Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.3 - Ex. 10

Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral.

a s   r e t a s     y = 1 - x ,   e   y = 2 ,   e   a   c u r v a   y = e x

Passo 1

Faaaala, cara! Tranquileba?

Fazendo um esboço das funções, temos:

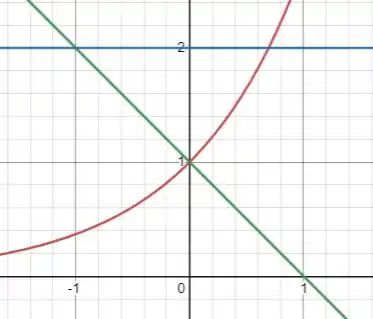
Analisando a figura, vemos que 1 ≤ y ≤ 2 e fazendo x em função de y e x = y → x = ln ⁡ y   temos 1 - y ≤ x ≤ l n ⁡ ( y ) . Logo:

∫ 1 2 ∫ 1 - y ln ⁡ y d x d y

Passo 2

∫ 1 2 ln ⁡ y - 1 - y d y

∫ 1 2 ln ⁡ y d y - ∫ 1 2 d y + ∫ 1 2 y   d y

Passo 3

Para:

∫ 1 2 ln ⁡ y d y

Façamos u = ln ⁡ y logo d u = 1 y e v = x logo d v = d x . Assim:

∫ 1 2 u   d v

Das técnicas de integração temos que:

∫ u   d v = u v - ∫ v   d u

Assim:

y ln ⁡ y 1 2 -   ∫ 1 2 d y

y ln ⁡ y - y 1 2

Assim:

y ln ⁡ y - y - y 1 2 + 1 2 y 2 1 2

  y ln ⁡ y - 2 y + y 2 2 1 2

2 ln ⁡ 2 - 1 2

Resposta

2 ln ⁡ 2 - 1 2

Exercícios de Livros Relacionados

Calcule a integral dupla. ∬ D e - y 2 d A ,D = x , y | 0 ≤ y ≤ 3 ,0 ≤ x ≤ y
Calcule a integral dupla. ∬ D x 2 + 2 y d A , Dél i m i t a d ap o ry = x , y = x 3 ,x ≥ 0 é
Defina as integrais iteradas para ambas as ordens de integração. Então, calcule a integral dupla usando a ordem mais fácil e explique porque ela é mais fácil. ∬ D y d A , Dél i m i t a d ap o ry = x -
Calcule a integral dupla. ∬ D y x 2 - y 2 d A ,D = x , y | 0 ≤ x ≤ 2 ,0 ≤ y ≤ x
Calcule a integral dupla. ∬ D y x 2 + 1 d A ,D = x , y | 0 ≤ x ≤ 4 ,0 ≤ y ≤ x