Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 18
Calcule a integral dupla.
Passo 1
Fala, amigos! De boa?
A questão pede para calcularmos a integral dupla:
Onde é limitada por:
Temos que começar nossa questão usando a região para conseguirmos nossos limites de integração para e . Se tivermos o gráfico da nossa região essa análise fica mais fácil.
Depois, podemos resolver a integral dupla em relação a e a , usando a ordem que tornar a integral mais fácil. Daí é só resolvermos a integral dupla como uma integral iterada.
Uma integral iterada é uma integral calculada sequencialmente, uma após a outra. Para resolver integrais duplas a gente começa “de dentro pra fora”.
Vem comigo!
Passo 2
O primeiro passo é esboçar as curvas que delimitam a região, para podermos avaliar nossa estratégia:
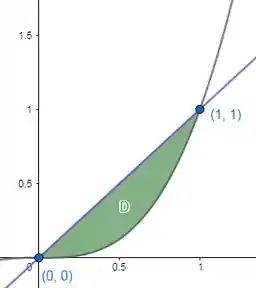
Vamos avaliar os limites de :
Logo, desde que temos que , . Portanto:
Passo 3
Agora, podemos tirar de:
Nossos limites de integração. Assim, a integral dupla pode ser escrita como:
Aqui, como o limite de integração de tem termos que dependem de , podemos colocar a integral de “por dentro”, assim simplifica nossos cálculos.
Vamos resolver a integral de dentro:
Logo:
Passo 4
Agora é só resolver:
Logo:
Portanto: