Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.8 - Ex. 115
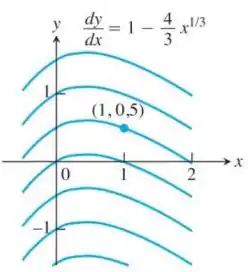
Os Exercícios 115-118 mostram curvas solução para equações diferenciais. Em cada exercício, determine uma equação para a curva através do ponto marcado.
Passo 1
Dada a primeira derivada da função da curva (também pode ser considerada o coeficiente angular) é possível encontrar a função primitiva a partir da integral da equação diferencial.
Ainda, para descobrir a constante que irá surgir após integrar a função, aplica-se as coordenadas do ponto dado.
Passo 2
Assim, a partir da equação diferencial, temos:
Passo 3
Aplicando a condição inicial na função primitiva encontrada:
.
Resposta
A equação da curva é .
Exercícios de Livros Relacionados
o) ∫ cos x 3 d x
j) ∫ 1 e 3 x d x
n) ∫ s e nx 2 d x
g) ∫ (x 2 +s e nx )d x
f) ∫ ( e 2 x + e - 2 x )d x