Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 3

Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano xy. Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o gráfico de cartesiana (os gráficos irão variar confor-

me a equação utilizada). Indique a parte do gráfico percorrida pela partícula e a direção do movimento.

Passo 1

Fala galerinha tranquilidade, essa parte de parametrizar significa que as função tem um parâmetro em comum, e ambas são escritas com base nesse parâmetro, o nosso papel ao resolver essas questões vai ser isolar o parâmetro em ambas função e igualar as duas, feito isso podemos apenas colocar x em função de y ou o contrário, e apenas esboçar o gráfico, usando algum tipo de software ou na mão mesmo dependendo da complexidade:

Passo 2

Nesse passo vamos isolar o parâmetro.

Passo 3

Agora só precisamos igualar ficando:

Agora vai depender do que for necessário para manipular, em alguns casos mais complexos será demonstrado, nós mais simples vamos para o resultado.

Resposta

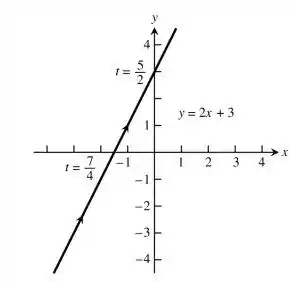
Aqui vamos colocar o gráfico em função do parâmetro e identificar para onde a função cresce:

Exercícios de Livros Relacionados

Use os gráficos de x = f ( t ) y = g ( t ) Para esboçar a curva paramétrica x = f ( t ) y = g ( t ) Indique com setas a direção na qual a curva é traçada à medida que t aumenta.

Encontre equações paramétricas para a elipse x 2 a 2 + y 2 b 2 = 1 Use as equações paramétricas para traçar a elipse quando a = 3 e b = 1 ,2 ,4e8 Como muda o formato da elipse quando b varia?

Mostre que as equações paramétricas x = x 1 + x 2 - x 1 t y = y 1 + y 2 - y 1 t Onde 0 ≤ t ≤ 1 descrevem o segmento de reta que une os pontos P 1 ( x 1 , y 1 ) e P 2 ( x 2 , y 2 ) .E encontre as equaç

Use os gráficos de x = f ( t ) y = g ( t ) Para esboçar a curva paramétrica x = f ( t ) y = g ( t ) Indique com setas a direção na qual a curva é traçada à medida que t aumenta.

Usando uma ferramenta gráfica e o resultado do Exercício 31, desenhe o trângulo com vértices A 1,1 ,B 4,2eC ( 1,5 ) .