Enunciado
Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.10 - Ex. 20
Siga as instruções do Exercício 19, se a .
Passo 1
Para a equação ser verdade, . Logo, seja
Para achar a raiz, pelo método de Newton, faremos aproximações sucessivas utilizando a fórmula: . Calculando teremos:
Passo 2
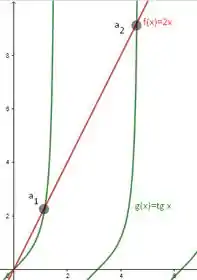
Observando o gráfico, vemos que, para achar utilizando o método de Newton, um bom valor de é 1.
Passo 3
Como , o valor de
Passo 4
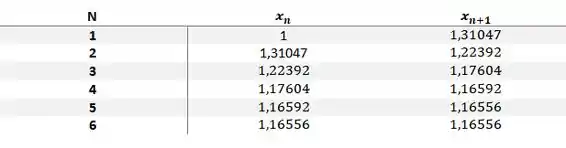
Para encontrar , utilizaremos o mesmo método, mas agora utilizaremos (observando o gráfico). A tabela ficará da seguinte forma:
Passo 5
Como , o valor de
Resposta
Exercícios de Livros Relacionados
Método de Newton Modificado:Existe uma modificação no método de Newton na qual a função de iteração φ ( x ) é dada por φ ( x ) = x - f ( x ) f ' ( x 0 ) onde x 0 é a aproximação inicial e é tal que f
Seja f ( x ) = x 2 2 + x ( l n ( x ) - 1 ) . Obtenha seus pontos críticos com o auxílio de um método numérico.
O valor de π pode ser obtido através da resolução das seguintes equações: s e n ( x ) = 0 c o s ( x ) + 1 = 0 Aplique o método de Newton com x 0 = 3 e precisão 1 0 - 7 em cada caso e compare os result
O polinômio p ( x ) = x 5 - 10 9 x 3 + 5 21 x tem seus cinco zeros reais, todos no intervalo (-1,1).Verifique que x 1 ∈ ( - 1 , - 0.75 ) ,x 2 ∈ ( - 0.75 , - 0.25 ) ,x 4 ∈ ( 0.3,0.8 )ex 5 ∈ ( 0.8,1 ) .
Seja f ( x ) = x e - x - e - 3 verifique gráfica e analiticamente que f(x) possui um zero no intervalo [0,1]; justifique teoricamente o comportamento da seqüência {xk} colocada a seguir, gerada pelo m