Em cada parte, encontre todos os pontos críticos e use o teste da derivada primera para classifica-los em máximos ou mínimos relativos, ou nenhum dos dois.

(b)

1. Considerando a função:

Para aplicar o teste da primeira derivada, devemos derivar a função e encontrar os pontos críticos, para posteriormente fazer a classificação.

Vamos derivar a função, lembrando que a derivada da soma é soma das derivadas:

Com a ajuda de uma ferramenta gráfica para analisar os pontos em que a função corta o eixo das no intervalo dado:

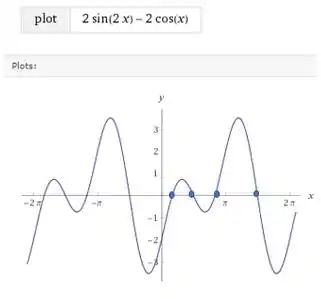
Esses valores são:

Esses pontos são as raízes da nossa função.