Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 14
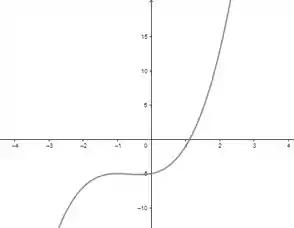
Nos exercícios de 13 a 32, faça um esboço do gráfico da função f dada, determinando primeiro o seguinte: os extremos relativos de f; os pontos de inflexão do gráfico; os intervalos nos quais f é crescente e aqueles onde f é decrescente; onde o gráfico é côncavo para cima e onde é côncavo para baixo; a inclinação das tangentes inflexionais, assíntotas horizontal, vertical e oblíqua, se existirem.
Passo 1
Seja . Vejamos que:
Logo, como tem que ser positivo. Logo, se existe raiz, ela é positiva.
Como não temos um método fácil de obtenção de raízes em um polinômio do 3º grau, começaremos testando raízes inteiras. Dessa forma, como o polinômio só tem coeficientes inteiros, a raiz tem que ser divisora de ou seja, divide Os possíveis valores de serão Começando pelo mais simples, testaremos
Logo, não tem raízes racionais. Dessa maneira, fazendo aproximações pelo teorema de Bolzano, encontraremos entre quais valores inteiros está a raiz. Pelo visto acima, como há troca de sinais, está entre 1 e 5.
Assim, temos que a raiz do polinômio está entre 1 e 2.
Passo 2
Calculando , teremos:
Pela Fórmula de Bhaskara, teremos:
Dessa forma, teremos que:
Dessa maneira, teremos que:
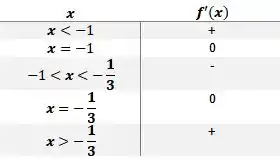
Passo 3
Calculando , teremos:
Daí, temos que a raiz de é
Além disso, temos que a tangente inflexional é
Passo 4
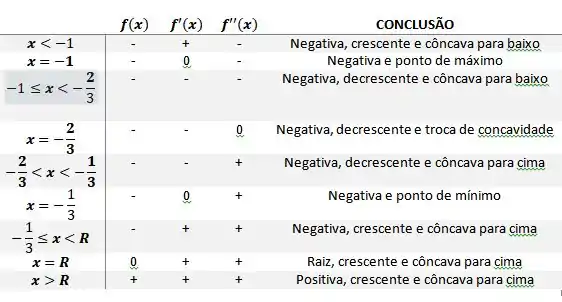
Passo 5
A partir dos dados coletados, teremos o seguinte gráfico:
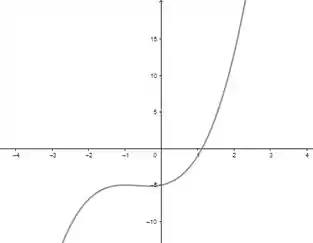
E os valores de máximo e mínimo relativos são, respectivamente, e
Resposta
Os extremos relativos de .
O ponto de inflexão de .
A função é crescente em e decrescente em .
O gráfico é côncavo para baixo em e côncavo para cima em .
A inclinação da tangente inflexional é .
Gráfico:
