Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.5 - Ex. 16
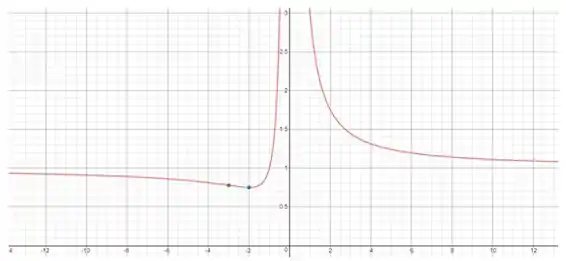
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Eaeee, belezinha??? Bom... A questão pede para usarmos a roteiro apresentado na seção do livro para fazer um esboço da curva.
Para iniciar a questão vamos relembrar um pouco da teoria:
Domínio: Conjunto de todos os valores de para os quais a função é definida.
Interseções com os Eixos:
- Eixo : Onde
- Eixo : Onde ou seja,
Simetria:
- Função Par:
- Função Ímpar:
Assíntotas:
- Assíntotas Verticais: Linhas verticais onde a função cresce sem limites.
- Assíntotas Horizontais: Linhas horizontais que a função se aproxima conforme
Derivadas e Comportamento da Função:
- Primeira Derivada Para determinar onde a função é crescente ou decrescente.
- Segunda Derivada Para determinar a concavidade e pontos de inflexão.
Os intervalos nos quais uma função é crescente (ou decrescente) correspondem aos intervalos nos quais sua derivada é positiva (ou negativa). Então, se quisermos encontrar os intervalos em que uma função é crescente ou decrescente, nós calculamos sua derivada e descobrimos onde ela é positiva ou negativa (o que é mais fácil!).
Concavidade e Pontos de Inflexão:
- Concavidade para cima:
- Concavidade para baixo:
- Pontos de Inflexão: Onde e muda de sinal.
Bora lá!! 😉
Passo 2
O domínio da função é onde o denominador não é zero.
Portanto, o domínio é
Passo 3
Para encontrarmos a interceptação, temos
- Intecepto
Para encontrar o intercepto definimos
- Intecepto
Para encontrar o intercepto definimos
Multiplicamos ambos os lados por
Não há soluções reais para esta equação, pois o discriminante
É negativo.
Portanto, não há intercpto .
Passo 4
Para determinar a simetria da função
Precisamos analisar a função para
Existem três tipos comuns de simetria que podemos verificar: simetria em relação ao eixo y, simetria em relação à origem e simetria em relação a uma linha y = c (em geral, assíntota horizontal).
Uma função é simétrica em relação ao eixo y se:
Vamos calcular para a função
Claramente,
Portanto, a função não é simétrica em relação ao eixo
Passo 5
Simetria em relação à origem
Uma função é simétrica em relação à origem se:
Vamos comparar com
Novamente,
Portanto, a função não é simétrica em relação à origem.
Passo 6
Simetria em relação a uma linha
A função tem uma assíntota horizontal em
Verificamos a simetria em relação a essa linha testando:
Se for ímpar, a função é simétrica em relação a
Vamos considerar
Agora calculamos
Para testar se é ímpar, comparamos:
Portanto,
Assim, a função
Não possui simetria em relação ao eixo y, à origem ou à linha
A função não possui nenhuma das simetrias comuns (nem em relação ao eixo y, nem à origem, nem à linha
Passo 7
Para as assíntotas horizontais, tomamos os limites no infinito:
Assim, tanto para como para , a reta é assíntota horizontal para a função.
Como não está no domínio da função, temos que verificar se essa reta é assíntota vertical. De fato,
Assim, a reta é assíntota vertical da função.
Passo 8
Para os intervalos de crescimento e decrescimento, precisamos da derivada da função. Assim,
O sinal de será:
Assim, o ponto é ponto de mínimo local. Note que não é ponto de máximo pois ele não pertence ao domínio da função.
Passo 9
No estudo da concavidade, precisamos de :
Como , segue que o sinal de vai depender apenas de :
O ponto será ponto de inflexão.
Resposta
O esboço da curva:
