Nos exercícios e , despreze a resistência do ar e tome .
Uma menina atira uma bola horizontalmente do topo de um penhasco de metros de altura, com uma velocidade inicial de . Calcule: (a) o tempo de trajeto da bola e (b) a distância desde a base do penhasco até o ponto em que a bola atinge o solo.
Passo 1
Show galera. Num lançamento horizontal, podemos resumir os vetores envolvidos na seguinte imagem:
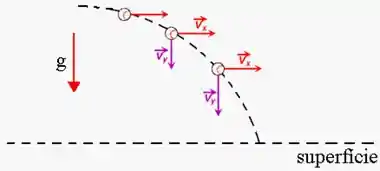
Seja o vetor posição , pra gente montar ele, vamos pensar em cada eixo. O eixo não possui aceleração, mas possui velocidade constante:
Oras galera, derivada constante? Só é possível se:
Se no intante inicial a bola está no mesmo lugar da menina, estabelecendo ela como temos:
Agora pro eixo , temos aceleração constante:
Manipulando:
No instante inicial a bola ainda tá na mão da menina, então a gravidade não começou a atuar ainda. Logo:
Seguindo essa lógica de novo pra achar , temos:
No instante inicial a bola está a de altura, então:
E o vetor posição é:
Passo 2
Show, agora vamos responder as letras (a) e (b) com base no vetor posição. Galera, vou chamar de o alcance da bolinha em relação a menina. Sendo assim, a posição final desse movimento vai ser:
Pra achar basta igualar ao vetor posição:
Continuando a manipulação, temos:
Feshow galera, com as unidades de medida, temos: