Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.5 - Ex. 11

Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (11) A parábola y = x ³ e a reta y = 4 x mo primeiro quadrante.

Passo 1

O primeiro passo é encontrarmos os pontos de intersecção entre y = x ³ e a reta y = 4 x . Assim:

4 x = x 3 x 3 - 4 x = 0 x x 2 - 4 = 0 x = 0   o u   x = ± 2

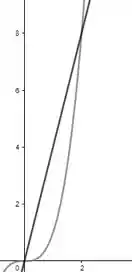
Passo 2

Vamos calcular a área da região delimitada elas duas funções.

A = ∫ 0 2 4 x - x 3 d x = 2 x 2 - x 4 4 0 2   A = 2 * 2 2 - 2 4 4 A = 8 - 4 = 4

Passo 3

Calculando agora o valor de m x e m y .

m x = 1 2 ∫ 0 2 ( 4 x - x 3 ) ( 4 x + x 3 ) d x = 1 2 ∫ 0 4 ( 16 x 2 - x 6 ) d x m x = 1 2 16 x 3 3 - x 7 7 0 2 = 1 2 16 * 2 3 3 - 2 7 7 m x = 256 21

m y = ∫ 0 2 x 4 x - x 3 d x = ∫ 0 4 4 x 2 - x 4 d x m y = 4 x 3 3 - x 5 5 0 2 = 4 * 2 3 3 - 2 5 5 m y = 64 15

Passo 4

Vamos agora encontrar agora os pontos do centróide.

y - = 1 A m x = 1 4 * 256 21 y - = 64 21

x - = 1 A m y = 1 4 * 64 15 x - = 16 15

Resposta

O centróide está localizado no ponto 16 15 , 64 21 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = 1 4 x 2 , y = 2 x 2 , x + y = 3 ,x ≥ 0
Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas. y = x x 2
Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas. y = e x ,
Represente graficamente a região entre as curvas e use a calculadora para encontrar a área correta até a quinta casa decimal. y = cos ⁡ x ,y = x + 2 sin 4 ⁡ x
Calcule a integral, interpretando-a em termo de áreas. ∫ - 5 5 x - 25 - x 2 d x