Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.8 - Ex. 2
Nos Exercícios 1-4:
a. Determine .
b. Esboce em um único gráfico e .
c. Calcule em e em para mostrar que nesses pontos .
2.
Passo 1
a. Determinando , temos:
Agora voltando as variáveis para o formato convencional, que é , teremos:
Passo 2
b. Se esboçarmos o gráfico de e , teremos:
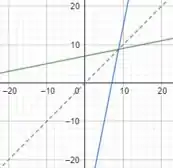
No qual é a função verde, é a função azul e a função pontilhada é .
Passo 3
c. Calculando a derivada da função que nos foi cedida, teremos:
De acordo com o George na seção 8, temos que:
Dessa forma, fica provado que nesses pontos, de fato, é válido.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Ache ( f - 1 ) ' ( d ) . f x = x 2 - 16 ;d = 9
Nos exercícios de 29 a 34, faça o seguinte: ( a ) resolva a equação para y em termos de x e expresse y como uma ou mais função de x ; ( b ) para cada função obtida em ( a ) determine se a função tem i
Nos exercícios de 29 a 34, faça o seguinte: ( a ) resolva a equação para y em termos de x e expresse y como uma ou mais função de x ; ( b ) para cada função obtida em ( a ) determine se a função tem i
Nos exercícios de 29 a 34, faça o seguinte: ( a ) resolva a equação para y em termos de x e expresse y como uma ou mais função de x ; ( b ) para cada função obtida em ( a ) determine se a função tem i
Ache ( f - 1 ) ' ( d ) . f x = x 3 + 5 ;d = - 3