Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 21

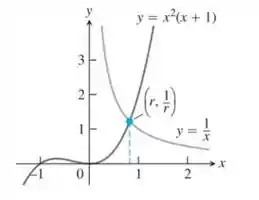
As curvas y   =   x 2 ( x   +   1 ) e y   = 1 x   ( x   >   0 ) se cruzam em um ponto x   =   r . Use o método de Newton para estimar o valor de r com quatro casas decimais.

Passo 1

Desejamos encontrar o ponto de encontro entre as duas curvas, ou seja, o ponto que o enunciado chamou de r é o ponto que satisfaz a seguinte equação

x 2 ⋅ x + 1 = 1 x → f x = x 3 + x 2 - 1 x

Queremos aplicar o método de Newton para encontrar a raiz dessa função, esse método nos diz que

x n + 1 = x n - f ( x n ) f ' ( x n )

Observando o gráfico percebemos que o valor de r se encontra próximo a 1, então, usaremos esse valor como nosso x 0 .

Passo 2

Para aplicarmos o nosso método, primeiramente vamos derivar a função que nos foi dada, assim, teremos

f x = x 3 + x 2 - 1 x → f ' x = 3 x 2 + 2 x + 1 x 2

Substituindo na nossa fórmula, vamos obter

x n + 1 = x n - x n 3 + x n 2 - 1 x n 3 x n 2 + 2 x n + 1 x n 2

Tomando x 0 = 1 temos

x 0 + 1 = x 0 - x 0 3 + x 0 2 - 1 x 0 3 x 0 2 + 2 x 0 + 1 x 0 2

x 1 = 1 - 1 3 + 1 2 - 1 1 3 ⋅ 1 2 + 2 ⋅ 1 + 1 1 2

x 1 = 1 - 1 6

x 1 ≈ 0.8333

Repetindo o procedimento, mas agora com x 1 = 0.8333 encontraremos

x 2 ≈ 0.8 1924

x 3 ≈ 0.8 1917

… .

x 7 ≈ 0.8 1917

Portanto, com a aproximação de quatro casas decimais podemos escrever r como sendo

r ≈ 0.8192

Passo 3

r ≈ 0.8192

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para que valor(es) de x teremos e - x 2 = x 2 - x + 1 ?
Nos problemas para localizar submarinos, normalmente é necessário determinar o ponto de aproximação máxima (PAM) em relação a uma sonoboia ( equipamento eletrônico flutuante que capta sinais sonoros d
Use o teorema do valor intermediário para mostrar que f ( x )=x 3+2 x-4 tem uma raiz entrex=1 e x =2 . Em seguida, determine a raiz com cinco casas decimais.
Algumas curvas são tão planas que, na prática, o método de Newton para demasiado longe da raiz para fornecer uma estimativa útil. Tente usar o método de Newton em f ( x )=x-140 com uma estimativa inic
Os gráficos de y= x e y=3-x 2 se cruzam em um ponto x=r . Use o método de Newton para calcular o valor de r com quatro casas decimais.