Enunciado
Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.10 - Ex. 17
Nos exercícios de 15 a 18, use o método de Newton para encontrar, com quatro casa decimais, a coordenada x do ponto de interseção no primeiro quadrante dos gráficos das duas equações.
Passo 1
Fazendo , teremos o gráfico abaixo:
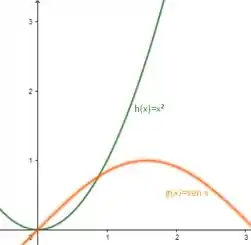
Para que haja interseção, devemos observar que , dessa maneira, Com isso, podemos considerar e achar a raiz dessa função no primeiro quadrante.
Passo 2
Pelo Método de Newton, temos que Calculando temos que:
Passo 3
Analisando o gráfico, vemos que uma e escolha razoável é . Utilizando a relação do método, formaremos a seguinte tabela:
Passo 4
Como , temos que a raiz aproximada de é 0,8767.
Resposta
Exercícios de Livros Relacionados
Encontrar as dimensões de um retângulo que possui um lado no eixo x , um lado adjacente a esse no eixo y , o vértice em comum a esses lados na origem e o vértice oposto a ele na curva y = ln x x 2 ,
Nos exercícios 21 e 22, obtenha uma aproximação de π com cinco casas decimais, usando o Método de Newton para resolver a equação.
Nos exercícios de 15 a 18, use o método de Newton para encontrar, com quatro casa decimais, a coordenada x do ponto de interseção no primeiro quadrante dos gráficos das duas equações.
Equações da forma t gx + a x = 0 , onde a é inteiro, surgem em problemas de condução de calor. As raízes positivas da equação em ordem crescente são a 1 ,a 2 ,a 3 , … Se a = 1 , ache a 1ea 2 com quatr