Nos exercícios 21 e 22, obtenha uma aproximação de com cinco casas decimais, usando o Método de Newton para resolver a equação.
Passo 1
Seja a função . Seu gráfico é da seguinte forma:
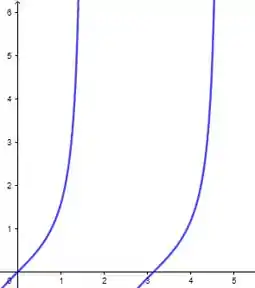
Sabemos que e é a primeira raiz positiva. Dessa forma, faremos aproximação pelo método de Newton.
Logo, calculando , teremos:
Passo 2
Pelo gráfico, uma escolha razoável parece Utilizaremos a relação , teremos de acordo com a seguinte tabela:

Passo 3
Como são iguais a 3,141592, temos que a raiz aproximada, ou seja, .