Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.3 - Ex. 30

Nos Exercícios de 15-34, use qualquer método para calcular as integrais. A maioria exigirá substituições trigonométricas, mas algumas podem ser calculadas por outros métodos.

30.

∫ 6 d t ( 9 t 2 + 1 ) 2

Passo 1

O enunciado pede para gente calcular o valor dessa integral.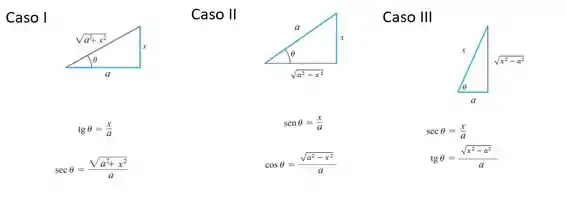

Vamos usar essa imagem de referência para os casos onde serão necessárias substituições trigonométricas.

Esse caso se encaixa no caso I.

Passo 2

Vamos usar a substituição onde

t = 1 3 t g   u d t = 1 3 ⁡ s e c 2 u   d u

Lembrando também a relação trigonométrica

Vamos usar também a relação trigonométrica onde

1 + t g 2 ѳ = s e c 2 ѳ

E aí podemos dizer que

9 t 2 + 1 = sec 2 ⁡ u

E aí nossa integral fica

∫ 6 d t ( 9 t 2 + 1 ) 2 = 6 ∫ 1 3 ⁡ s e c 2 u   d u s e c 4 u       = 2   ∫ 1 s e c 2 u d u = 4 ∫ c o s 2 u d u

Passo 3

Agora vamos resolver essa integral

Primeiro vamos lembrar que

c o s 2 ѳ = 1 + cos ⁡ 2 ѳ 2

Então

2 ∫ c o s 2 u d u = ∫ d u + ∫ cos ⁡ 2 u   d u

Vamos resolver a primeira integral

∫ d u = u + C

Agora a segunda integral

∫ cos ⁡ 2 u   d u

Vamos fazer a substituição

v = 2 u d v = 2 d u

Então

∫ cos ⁡ 2 u   d u = 1 2 ∫ cos ⁡ v   d v = 1 2 s e n   v + C = 1 2 s e n 2 u + C

Nossa integral fica

∫ d u + ∫ cos ⁡ 2 u   d u = u + 1 2 s e n   2 u + C = u + s e n   u ⋅ cos ⁡ u + C

Passo 4

Mas t = 1 3 t g   u    

1 + t g 2 u = 1 c o s 2 u , então c o s 2 u = 1 1 + t g 2 u

E s e n 2 u = 1 - c o s 2 u

Logo

s e n 2 u = 1 - 1 1 + 9 t 2

c o s 2 u = 1 1 + 9 t 2

s e n   u ⋅ cos ⁡ u = 3 t 1 + 9 t 2

Então

u + s e n   u ⋅ cos ⁡ u + C = a r c t g   3 t + 3 t 1 + 9 t 2 + C

Resposta

a r c t g   3 t + 3 t 1 + 9 t 2 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Com uma conveniente mudança de variével, transforme a integral dada numa do tipob) ∫ x + 1 0 x 2 + 2 x + 2 d x
Calculem) ∫ x ( a r c t g x ) ² d x ²
Calcule a integral ∫ c o s 2 xc o s 6 xd x .
Calcule a integral. ∫ sin 5 ⁡ t cos 4 ⁡ t d t
Calcule a integral. ∫ 0 π t cos 2 ⁡ t d t