Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.8 - Ex. 10

Nos exercícios de 1 a 16, ache os extremos absolutos da função dada no intervalo indicado, se existir algum (10) f x = 3 x 4 - 2 x 3 - 12 x 2 - 6 x - 1 ; ( - ∞ , ∞ ) .

Passo 1

Vamos encontrar as derivadas primeira e segunda da função:

f ' x = 12 x 3 - 6 x 2 - 24 x - 6 f ' ' x = 36 x 2 - 12 x - 24

Passo 2

A primeira derivada vai nos indicar se há pontos críticos na função. Vamos igualar a expressão encontrada no passo anterior.

12 x 3 - 6 x 2 - 24 x - 6 = 0

Vamos fatorar o lado esquerdo da igualdade:

6 2 x 3 - x 2 - 4 - 1 = 0 Resolvendo Bhaskara para encontrar as raízes do polinômio de segundo grau:

6 x + 1 2 x 2 - 3 x - 1 = 0

Os valores críticos são x = - 1 ; 3 + 17 4 ; 3 - 17 4

Passo 3

Vamos avaliar os pontos críticos na segunda derivada para encontrarmos os pontos de mínimo ou máximo local.

  • Para x = - 1

    • f ' ' - 1 = 36 * - 1 2 - 12 * ( - 1 ) - 24 f ' ' x = 24

    x = - 1 é um mínimo local porque o valor da segunda derivada é positivo

  • Para x = 3 + 17 4

    • f ' ' 3 + 17 4 = 36 * 3 + 17 4 2 - 12 * 3 + 17 4 - 24 f ' ' 3 + 17 4 = 51 + 21 17 2

    x = 3 + 17 4 é um mínimo local porque o valor da segunda derivada é positivo

  • Para x = 3 - 17 4

f ' ' 3 - 17 4 = 36 * 3 - 17 4 2 - 12 * 3 - 17 4 - 24 f ' ' 3 - 17 4 = 51 - 21 17 4

x = 3 - 17 4 é um ponto de máximo local porque o valor da segunda derivada é negativo.

Passo 4

Avaliando na função os pontos extremos do nosso intervalo temos:

f x = x 4 3 - 2 x - 12 x 2 - 6 x 3 - 1 x 4 f - ∞ = - ∞ 4 3 - 2 - ∞ - 12 - ∞ 2 - 6 - ∞ 3 - 1 - ∞ 4 f - ∞ = ∞

f ∞ = ∞ 4 3 - 2 ∞ - 12 ∞ 2 - 6 ∞ 3 - 1 ∞ 4 f ∞ = ∞    

Em ambos extremos do intervalo podemos observar que o valor vai para o infinito positivo, o que nos leva a concluir que não há pontos de máximo absoluto nesse intervalo.

Vamos montar uma tabela com os resultados obtidos.

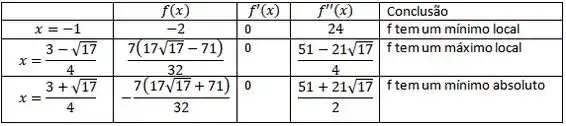
Resposta

Portanto, os valores extremos para a f ( x ) são:

x = - 1   c o m o   m í n i m o   l o c a l x = 3 - 17 4 c o m o   m á x i m o   l o c a l x = 3 + 17 4   c o m o   m í n i m o   a b s o l u t o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache os números críticos da função dada.f (t) = t^(5 // 3) - 3 t^(2 // 3)
Ache os números críticos da função dada.f (x) = x^3 + 7 x^2 - 5 x
Ache os números críticos da função dada.f (x) = x^(7 // 3) + x^(4 // 3) - 3 x^(1 // 3)
Ache os números críticos da função dada.f (x) = (x^3 - 3 x^2 + 4)^(1 // 3)
Ache os números críticos da função dada.f (x) = (x)/(x^2 - 9)