Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.6 - Ex. 21
Nos exercícios 18 a 24, representar geometricamente o campo gradiente definido pela função dada:
Passo 1
A ideia nesse exercício será encontrar o campo gradiente da função que ele nos deu usando aquela formula lá da teoria. E em seguida, representar geometricamente esse campo. Para encontrarmos o campo, fazemos o assim:
Como :
Assim,
Passo 2
Repare que a expressão do é apenas uma reta. Então, sua representação fica o seguinte:
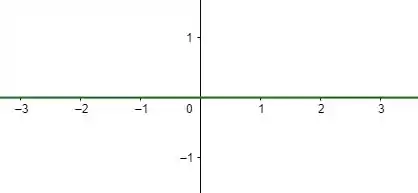
Resposta
Exercícios de Livros Relacionados
Determinar o vetor gradiente das funções dadas nos pontos indicados:h) z = x 2 + y 2s e n( x 2 + y 2 ) ; P 0,0
Nos exercícios 7 a 17, calcular o gradiente do campo escalar dado.7. f x ,y ,z = x y + x z + y z .
Nos exercícios 7 a 17, calcular o gradiente do campo escalar dado.17. f x ,y ,z = z e x 2 - y .
Nos exercícios 18 a 24, representar geometricamente o campo gradiente definido pela função dada:19. u x ,y = 2 x + 4 y .
Nos exercícios 7 a 17, calcular o gradiente do campo escalar dado.8. f x ,y ,z = x 2 + 2 y 2 + 4 z 2 .