Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.1 - Ex. 25
Nos exercícios de 19 a 40, determine se a função dada tem uma inversa. Se a inversa exisitir, determine-a e faça o seguinte: (a) ache o domínio e a imagem;(b) faça esboço de gráficos da função e de sua inversa, no mesmo conjunto de eixos. Se a função não tiver uma inversa, mostre que uma reta horizontal intercepta o gráfico da função em mais de um ponto.
25.
Passo 1
Primeiramente precisamos saber que uma função só possue inversa se for biunívoca, ou seja, para cada elemento da imagem existe apenas um elemento do domínio. Caso uma imagem tenha duas imagens do domínio diferentes no intervalo, então ela não é biunívoca, portanto não possui inversa.
Passo 2
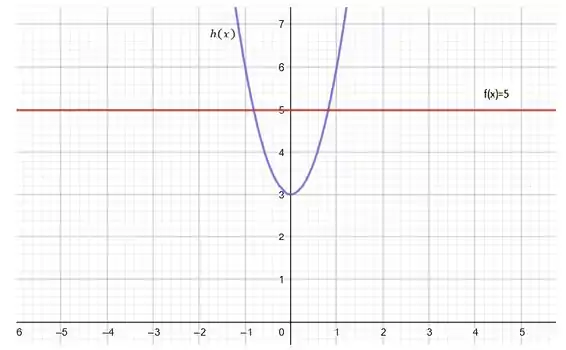
Essa função não possui uma inversa porque ela não é biunívoca. Portanto mostraremos apenas que uma reta horizontal toca o gráfico da função em dois pontos.
Passo 3
Como a função não possui inversa emboçaremos o gráfico com uma reta constante cruzando o gráfico em dois pontos.
Resposta
Essa função não possui inversa porque não é biunívoca.