Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.3 - Ex. 41
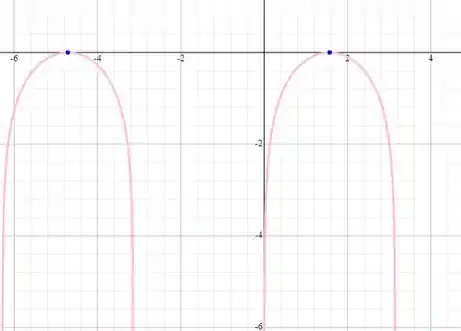
Nos exercícios de 34 a 41, faça um esboço do gráfico da curva com a equação dada.
41.
Passo 1
Neste tipo de questão, como estamos acostumados com uma função de y em função de x teremos que utilizar de alguns artifícios matemáticos para reescrever as funções dadas da forma adequada.
Para resolução também, é importante ter em mento o comportamento dos gráficos das funções .
Passo 2
Sendo assim, temos que o gráfico da função dada pode ser dado por:
Resposta
Exercícios de Livros Relacionados
Identidade para s e n - 1 x + c o s - 1 x = π 2 : A figura (1) estabelece a identidade para 0x1 . Para estabelecer a identidade para o restante de [-1,1], verifique, por cálculo direto, que ela é verd
Inicie o gráfico com y=l n x . Determine uma equação para o gráfico que resulte em uma translação de três unidades para baixo.
Inicie o gráfico com y=l nx . Determine uma equação para o gráfico que resulte em uma translação de 4 unidades para baixo e 2 unidades para a direita.
Inicie o gráfico com y=l n x . Determine uma equação para o gráfico que resulte em uma translação de três unidades para baixo.
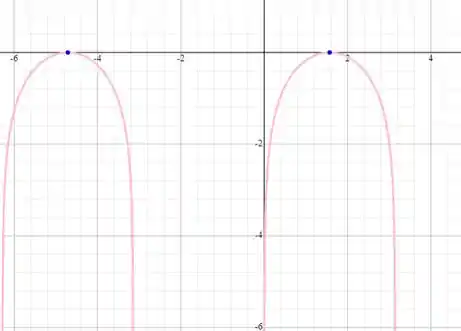
Inicie o gráfico com y=l n x . Determine uma equação para o gráfico que resulte em uma translação de 1 unidade para a esquerda e 3 unidades para cima.