Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 77

Seja P um ponto qualquer (exceto a origem) na curva r = f ( θ ) . Se ψ for o ângulo entre a reta tangente em P e a reta radial em O P mostre que

tan ⁡ ψ = r d r d θ

Sugestão: observe que ψ = ϕ - θ na figura.

Passo 1

Eaeee, belezinha??? Bom... o enunciado nos dá a seguinte curva r = f ( θ ) :

Aqui P é um ponto qualquer (exceto a origem).

Além disso, ψ é o ângulo entre a reta tangente em P e a reta radial em O P .

Com isso, queremos provar que

tan ⁡ ψ = r d r d θ

Então vamos ver se a gente consegue arrumar algum jeito de calcular tan ⁡ ψ pra ver se a gente chega nisso aí que a questão quer.

Tomara que sim né haha.

Ahh.. o enunciado ainda nos deu a seguinte dica:

ψ = ϕ - θ

Agora bora lá!! 😉

Passo 2

Como a própria questão sugere:

ψ = ϕ - θ

Então podemos dizer que

tan ⁡ ψ = tan ⁡ ( ϕ - θ )

Das fórmulas de subtração de arcos:

tan ⁡ ( ϕ - θ ) = tan ⁡ ϕ - tan ⁡ θ 1 + tan ⁡ ϕ tan ⁡ θ

Passo 3

Pela figura

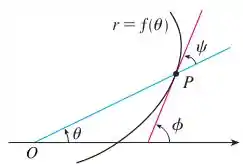
Como ϕ é a inclinação da reta tangente a curva em P , então podemos dizer que:

tan ⁡ ϕ = d y d x

Colocando essa derivada em termos do parâmetro θ da curva:

d y d x = d y d θ d x d θ

Passo 4

Voltando para a nossa equação:

tan ⁡ ( ϕ - θ ) = tan ⁡ ϕ - tan ⁡ θ 1 + tan ⁡ ϕ tan ⁡ θ ∴

tan ⁡ ( ϕ - θ ) = d y d θ d x d θ - tan ⁡ θ 1 + d y d θ d x d θ tan ⁡ θ

Fazendo o MMC em cima e em baixo:

tan ⁡ ϕ - θ = d y d θ - d x d θ tan ⁡ θ d x d θ d x d θ + d y d θ tan ⁡ θ d x d θ ∴

tan ⁡ ( ϕ - θ ) = d y d θ - d x d θ tan ⁡ θ d x d θ + d y d θ tan ⁡ θ  

Passo 5

Acontece que, em coordenadas polares:

x = r cos ⁡ θ

y = r sen ⁡ θ

Assim, derivando x e y em relação a θ , usando a regra do produto, ficamos com

d x d θ = d r d θ cos ⁡ θ - r sen ⁡ θ

E

d y d θ = d r d θ sen ⁡ θ + r cos ⁡ θ

Passo 6

Substituindo na nossa expressão da tangente:

tan ⁡ ϕ - θ = d y d θ - d x d θ tan ⁡ θ d x d θ + d y d θ tan ⁡ θ   ∴

tan ⁡ ( ϕ - θ ) = d r d θ sen ⁡ θ + r cos ⁡ θ - tan ⁡ θ d r d θ cos ⁡ θ - r sen ⁡ θ d r d θ cos ⁡ θ - r sen ⁡ θ + tan ⁡ θ d r d θ sen ⁡ θ + r cos ⁡ θ  

Fazendo as distributivas, chegamos em:

tan ⁡ ( ϕ - θ ) = d r d θ sen ⁡ θ + r cos ⁡ θ - d r d θ sen ⁡ θ + r sen 2 ⁡ θ cos ⁡ θ d r d θ cos ⁡ θ - r sen ⁡ θ + d r d θ sen 2 ⁡ θ cos ⁡ θ + r sen ⁡ θ   ∴

tan ⁡ ( ϕ - θ ) = r cos ⁡ θ + r sen 2 ⁡ θ cos ⁡ θ d r d θ cos ⁡ θ + d r d θ sen 2 ⁡ θ cos ⁡ θ  

Fazendo MMC:

tan ⁡ ϕ - θ = r cos 2 ⁡ θ + r sen 2 ⁡ θ d r d θ cos 2 ⁡ θ + d r d θ sen 2 ⁡ θ   ∴

tan ⁡ ( ϕ - θ ) = r ( cos 2 ⁡ θ + sen 2 ⁡ θ ) d r d θ ( cos 2 ⁡ θ + sen 2 ⁡ θ   ) ∴

tan ⁡ ψ = r d r d θ

UFA, PROVAMOS!!

Resposta

Demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o exercício 83 para mostrar que o ângulo entre a reta tangente e a reta tadial é ψ = π 4 em cada ponto na curva r = e θ .Ilustre a parte ( a ) traçando, com uma ferramenta gráfica, a curva e a ret
Use a fórmula no Exercício 69(b) para encontrar a curvatura da parábola y = x 2 no ponto ( 1,1 ) .Em que ponto essa parábola tem curvatura máxima?
Se f ' for contínua e f ' t ≠ 0 para a ≤ t ≤ b , mostre que a curva parametrizada x = f t , y = g t , a ≤ t ≤ b , pode ser colocada na forma y = F x . [Sugestão: Mostre que f - 1 existe.]
Use a fórmula no Exercício 69(a) para calcular a curvatura da cicloide x = θ - s e nθ , y = 1 - cos ⁡ θ no topo de um dos arcos.