Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.4 - Ex. 24

Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme indicado. Para cada exercício, faça uma figura

mostrando a região e o i-ésimo retângulo.

A região do Exercício 23; retângulos inscritos.

(região limitada por y   =   2 x , o eixo x e as retas x   =   1 e x   =   4 )

Passo 1

Para começar vamos determinar as extremidades do nosso problema:

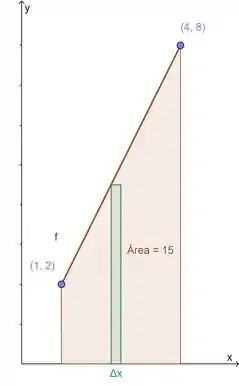
Nossa região está acima do eixo x sob a curva y = 2 x no intervalo fechado 1,4 .

Dividindo f x = 2 x em n subintervalos cada um com comprimento:

∆ x = 4 - 1 n = 3 n

Passo 2

Nosso i-ésimo subintervalo é [ x i - 1 , x i ] , onde i = 1 ,   2 ,   3 … ,   n .

Como o exercício nos pede a região por retângulos inscritos e f é crescente em nosso intervalo [ 1,4 ] , o valor mínimo absoluto de f em [ x i - 1 , x i ] é f ( x i - 1 ) . Logo a nossa área é dada por:

A = lim n → + ∞ ⁡ ∑ i = 1 n f x i - 1 ∆ x

Já que nosso intervalo começa em 1, teremos x i = 1 + ( i - 1 ) ∆ x

Como f x = 2 x ,

f x i = 2 x i

f x i = 2 ( 1 + ( i - 1 ) ∆ x )

Mas ∆ x = 3 n , assim:

f x i = 2 1 + ( i - 1 ) ⋅ 3 n

Passo 3

Aplicando o somatório de todos os subintervalos:

∑ i = 1 n f x i ∆ x = ∑ i = 1 n 2 1 + 3 ( i - 1 ) n ⋅ 3 n

= 6 n ∑ i = 1 n 1 + 3 ( i - 1 ) n

= 6 n ∑ i = 1 n 1 + 3 i n - 3 n

Utilizando as regras da soma ∑ k = 1 n k = 1 2 n ( n + 1 ) e ∑ k = 1 n a = a ⋅ n

= 6 n ⋅ n + 3 n n 2 n + 1 - 3 n ⋅ n

Finalmente, fazendo o limite quando n → + ∞ :

l i m n → ∞ 6 1 + 3 2 n n + 1 - 3

= l i m n → ∞ 6 1 + 3 2 n n 1 + 1 n - 3 n

= l i m n → ∞ 6 1 + 3 2 1 + 1 n - 3 n

= l i m n → ∞ 6 1 + 3 2 = 15    

A área da região é 15 unidades de área.

Passo 4

A figura abaixo mostra em verde a região o i-ésimo retângulo inscrito, onde a base é dada por ∆ x começando em x i - 1 e terminando em x i .

Resposta

A = 15   unidades de área.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que as desigualdades 12 e 13 não têm serventia para encontrar uma cota superior para o erro absoluto que resulta de aproximar a integral dada com as aproximações tanto pelo ponto médio quanto t
As medidas de um caco de cerâmica descoberto em uma escavação arqueológica revelam que ele veio de um pote com uma base plana e secção transversal circular (ver figura a seguir). A figura mostra medid
A tabela abaixo dá as velocidades em milhas por segundo em vários instantes para um foguete de teste lançado para cima da superfície da Terra. Use esses valores para aproximar o número de milhas perco
Use a aproximação S 10 da regra de Simpson para aproximar o comprimento da curva. Expresse sua resposta com pelo menos quatro casas decimais. y = s e n x ,d e s d ex = 0a t éx = π é
Encontre um valor de n que garanta que o erro absoluto na aproximação da integral com a aproximação pelo ponto médio seja inferior a 10 - 4 . Dê uma estimativa do erro absoluto e expresse suas respost