Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.3 - Ex. 40
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada.
40 ) Cone gerado pela semi reta quando esta gira em torno do eixo positivo dos y.
Passo 1
Então galera, desenhando nossa reta:
O ângulo entre a reta geratriz e o eixo y é , então do um ponto P qualquer sobre a reta:
Como:
Passo 2
Como o cone gira ao redor de y, teremos algo parecido com:
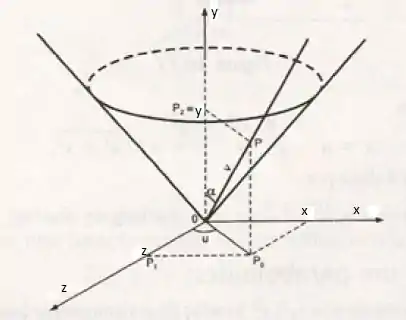
Do triângulo retângulo e
Do triângulo retângulo e
Agora que sabemos a parametrização do cone, basta substituir:
No cone, e v é limitado somente pelo zero,
Logo,
E encontramos nossa equação parametrizada!!
Resposta
Exercícios de Livros Relacionados
Encontre as equações paramétricas da superfície obtida pela rotação da curva y = 1 1 + x 2 , - 2 ≤ x ≤ 2 ao redor do eixo x e use-as para traçar o gráfico da superfície.
Encontre a área da superfície.Parte da superfície z = 4 - 2 x 2 + y que está acima do triângulo com vértices 0,0 ,( 1,0 ) e ( 1,1 ) .
Identifique a superfície com equação vetorial dada. r u , v = 1 + 2 u i + - u + 3 v j + 2 + 4 u + 5 v k
Identifique a superfície com equação vetorial dada. r u , v = u cos v i + u sen v j + u 2 k
Use um computador para traçar o gráfico da superfície paramétrica. Imprima o resultado e indique sobre ele quais são as curvas de grade que têm u constante e quais têm v costante. r u , v = cos 3 u