Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.6 - Ex. 7
Use um computador para traçar o gráfico da superfície paramétrica. Imprima o resultado e indique sobre ele quais são as curvas de grade que têm constante e quais têm costante.
Passo 1
E aiii minha turma fera, tudo bem com vocês!? Vamos nessa!
Nessa questão, devemos usar um software gráfico para traçar um esboço da superfície paramétrica abaixo:
Observe que é realmente complicado de fazer a mão um gráfico desse tipo.
Então vamos usar o Geogebra 3D para plotar.
Após plotar você avaliar as curvas de níveis na superfície da figura.
Bora lá resolver!
Passo 2
Precisamos esboçar a nossa superfície paramétrica.
Utilizando o software Geogebra 3D para nós auxiliares, temos:
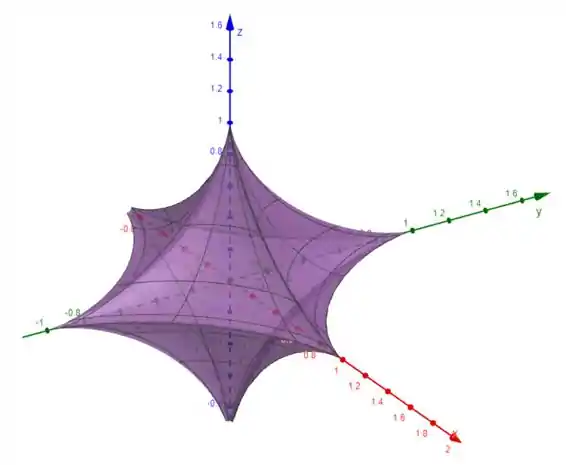
Caso queira plotar, use o seguinte input:
b=Superfície(cos^(3)(u) cos^(3)(v),sen^(3)(u) cos^(3)(v),sen^(3)(v),u,0,π,v,0,2 π)
A superfície representada é definida pelas seguintes equações paramétricas:
Curvas de constante:
Estas curvas são aquelas que são paralelas ao plano da base ().
Elas representam as linhas na superfície onde o valor de é fixo enquanto varia.
Curvas de constante:
Estas curvas são aquelas que pertencem a planos perpendiculares aos planos da base ( e ).
Elas representam as linhas na superfície onde o valor de é fixo enquanto varia.
Resposta
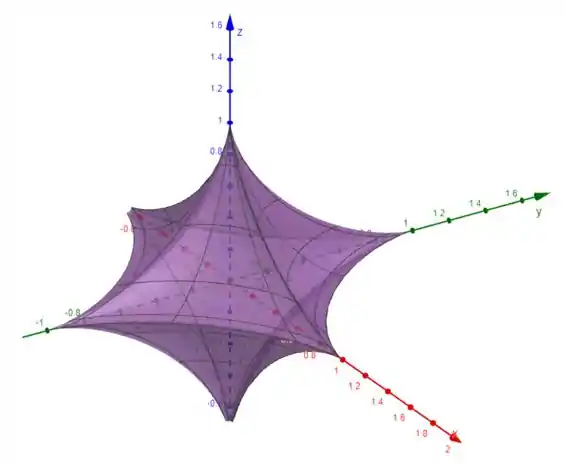
As curvas de grade que possuem constante são aquelas paralelas ao plano da base . Já as que possuem o valor de constante são aquelas que pertencem a planos perpendiculares aos planos da base ( e ).