Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.3 - Ex. 28
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada
Cone gerado pela semi-reta , quando esta gira em torno do eixo positivo dos
Passo 1
A equação do cone que gira em tore de é
Com os limites máximos: e
Passo 2
O ângulo que gira em torno de é . Como o gira é completo, então o limite de é:
Passo 3
O é o ângulo entre o eixo Z e a reta . Podemos utilizar relações geométricas para determinar o ângulo alpha.
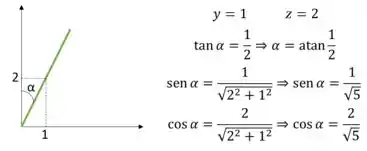
Passo 4
Podemos aplicar o valor do raio e de na equação do cone.
As componentes são:
Resposta
Exercícios de Livros Relacionados
Seja σ u , v = ( x , y , z ) , com x = u cos v , y = us e nv e z = u 2 . Mostre que σ transforma a faixa u ≥ 0 , 0 ≤ v ≤ 2 π , no paraboloide z = x 2 + y 2 .
Desenhe a imagem de σ u , v = u , v ,1 - u 2 - v 2 , com u 2 + v 2 ≤ 1 .
Desenhe a imagem de σ u , v = ( cos v ,s e nv ,u ) , com 0 ≤ u ≤ 1 e 0 ≤ v ≤ 2 π .
Seja σ u , v = ( x , y , z ) , com x = u cos v , y = us e nv e z = u .Mostre que a transformação σ transforma a reta u = u 1 ( u 1 ≠ 0 constante) numa circunferência. Desenhe tal circunferência no c
Seja σ u , v , w = ( u cos v ,us e nv ,w ) , 0 ≤ u ≤ 1 , 0 ≤ v ≤ 2 π e 0 ≤ w ≤ 1 . Desenhe a imagem de σ .