Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.1 - Ex. 6
Seja , com , e .
- Mostre que a transformação transforma a reta ( constante) numa circunferência. Desenhe tal circunferência no caso
- Mostre que σ transforma a reta ( constante) numa reta (no espaço xyz) passando pela origem.
- Desenhe onde é o retângulo
Passo 1
- Olha só, usando , nós temos o seguinte:
- Bom, se é constante, a gente tem:
- Bom, nesse caso a gente vai ter a partir do ponto várias circunferências, ou seja, temos um cone com vértice em e com área lateral sendo formada por vários círculos com raio variando de .
Quem manja um pouquinho de coordenadas polares vê que isso aí é uma circunferência de raio , centrada em . Pela equação já fica provado.
No caso da é uma circunferência de raio , centrada no plano . Eis o desenho:
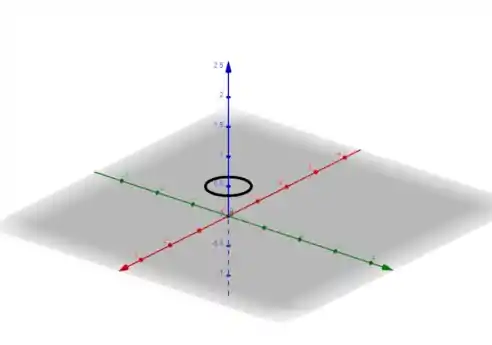
Passo 2
Nesse caso, a variável é somente , já que são valores constantes agora. Daí, como , temos o ponto pertencente a reta . Ou seja, é uma reta que passa pela origem.
Passo 3
Eis o desenho:
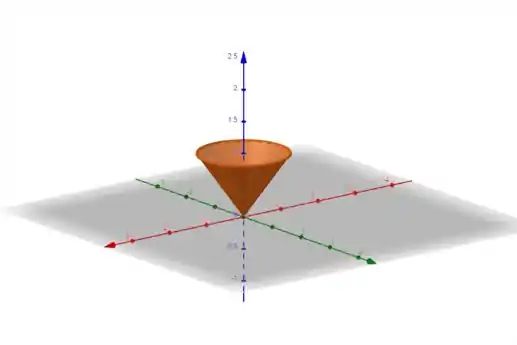
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada.40 ) Cone gerado pela semi reta y = 3 x ,x ≥ 0 , quando esta gira em torno do eixo positivo dos y.
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada z = 2 x 2 + y 2
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada x 2 + y 2 = 3
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada z = - 2 x 2 + y 2
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada x 2 + z 2 = 10