Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 1.1 - Ex. 9

Desenhe a imagem de sigma (u , v) = (u , v , sqrt(1 - u^2 - v^2)) , com u^2 + v^2 <= 1 .

Passo 1

Vamos reescrever essa transformação como:

{[[x = u],[y = v],[z = sqrt(1 - u^2 - v^2)]])

A gente pode colocar a última expressão toda em função de x , y e z , usando as duas de cima:

z = sqrt(1 - x^2 - y^2)

Vamos eliminar essa raiz...

z^2 = 1 - x^2 - y^2

x^2 + y^2 + z^2 = 1

Porém, veja que z >= 0 por causa da raiz. Então a superfície imagem é a semi-superfície esférica x^2 + y^2 + z^2 = 1 , z >= 0 .

Passo 2

Veja o desenho da imagem:

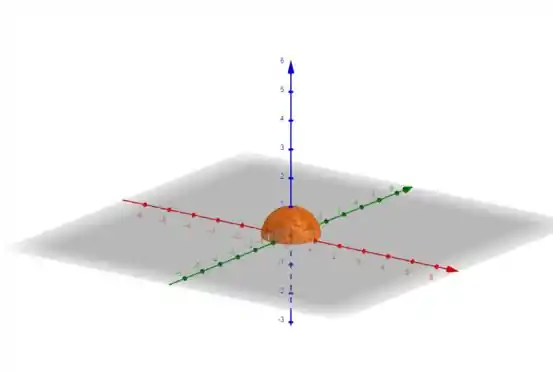
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use um computador para traçar o gráfico da superfície paramétrica. Imprima o resultado e indique sobre ele quais são as curvas de grade que têm u constante e quais têm v costante. r u , v = cos 3 ⁡ u
Case as equações com os gráficos identificados po I - V I e dê razões para sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. x = u 3 , y = sen ⁡ v , z
Use um computador para traçar o gráfico da superfície paramétrica. Imprima o resultado e indique sobre ele quais são as curvas da grade que têm u constante e quais tem v constante. x = u sen ⁡ u cos ⁡
A superficie com as equações parametricas x = 2 cos ⁡ θ + r cos ⁡ θ / 2 y = 2 sen ⁡ θ + r cos ⁡ θ / 2 z = r sen ⁡ θ / 2 Onde - 1 2 ≤ r ≤ 1 2 e 0 ≤ θ ≤ 2 π , é chamada Tira de Mobius. Trace o gráfico d
Case as equações com os gráficos identificados po I - V I e dê razões para sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante. r u , v = ucos ⁡ v i + u s