Desenhe a imagem de , com e
Passo 1
Olha só, aqui a gente tem o seguinte:
Bom, isso é coordenada polar. A gente tem o variando de , ou seja, o varia de e o estão variando de acordo com o seno e cosseno, de . Isso nos resulta em uma superfície cilíndrica, com altura variando de :
O desenho da imagem então é:
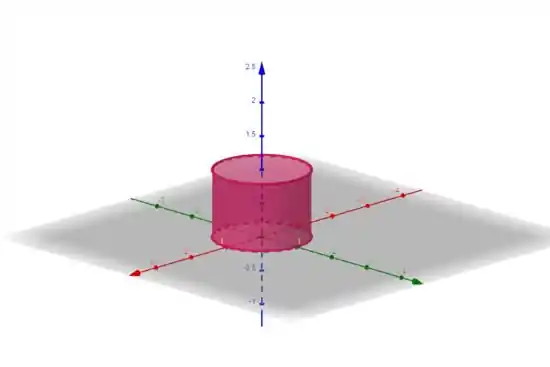
Resposta
Ei, a resposta está no passo a passo :)