Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.3 - Ex. 23

Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dada

Parte da esfera x 2 + y 2 + z 2 = 8 que está no 2 º octante

Passo 1

Os dados da questão: x 2 + y 2 + z 2 = 8 A esfera dada é centrada na origem e com raio a = 8 Os limites da esfera é o segundo octante. A imagem mostra que é a região delimitado por x < 0 ,   y > 0   e   z > 0 :

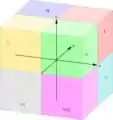
Em outros termos, é a região em que:

π 2 < u < π

0 < v < π 2

Passo 2

A equação da efera centrada na origem é:

r → ( u , v ) e s f e r a   n a o r i g e m = a cos ⁡ v cos ⁡ u i → + a cos ⁡ v sen ⁡ u j → + a sen ⁡ v k →

Substituíndo o valor do raio:

r → ( u , v ) = 2 2 cos ⁡ v cos ⁡ u i → + 2 2 cos ⁡ v sen ⁡ u j → + 2 2 sen ⁡ v k →

As componentes são:

x ( u , v ) = 2 2 cos ⁡ v cos ⁡ u

y ( u , v ) = 2 2 cos ⁡ v sen ⁡ u

z ( u , v ) = 2 2 sen ⁡ v

Resposta

x ( u , v ) = 2 2 cos ⁡ v cos ⁡ u

y ( u , v ) = 2 2 cos ⁡ v sen ⁡ u

z ( u , v ) = 2 2 sen ⁡ v

π 2 < u < π

0 < v < π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaParte da esfera x 2 + y 2 + z 2 = 1 que está entre os semiplanos y = x e y = 2 x , x ≥ 0
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaParte da esfera x 2 + y 2 + z 2 = 36 , tal que x ≥ 0 e y ≤ 0
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaCilindro x 2 - 2 x + y 2 - 6 y = 3
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaCilindro y 2 + z 2 = 9 , 0 ≤ x ≤ 4
Nos exercícios 21 a 45, escrever uma representação paramétrica para a superfície dadaA parte da esfera x 2 + y 2 + z 2 - 4 z = 0 que está acima do plano z = 2