Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 20
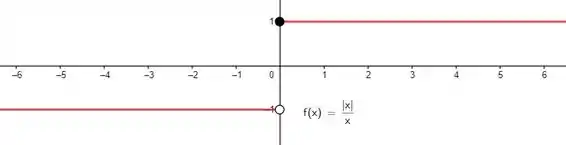
Nos exercícios de a , faça um esboço do gráfico da função; então, observando onde há quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre por que a Definição não é satisfeita em cada descontinuidade
Passo 1
Partiu então. Olha, a primeira coisa a se fazer com uma função dessas é destrinchar ela. Da definição de módulo:
Devidindo tudo por :
Podemos então reescrever a função:
E olha só! Essa função no final das contas nem depende de ! São dois números só, e diferentes. Como pra ter continuidade tinha que ser válido:
E nesse caso não temos isso, podemos afirmar que essa função não é contínua em !
Passo 2
Pra esboçar essa função só precisamos traçar as retas constantes e
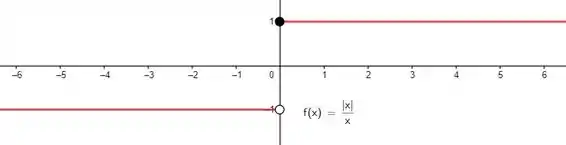
Resposta
Função não é contínua em
Exercícios de Livros Relacionados
Calcule p de modo que as funções abaixo sejam contínuas. f x = e 2 x , x ≠ 0 p 3 - 7 , x = 0
Determine, se existirem, os valores de x ∈ D f , nos quais a função f x não é contínua. f x = 2 e x - e - x
Determine, se existirem, os valores de x ∈ D f , nos quais a função f x não é contínua. f x = x x 2 - 1 ,x 2 ≠ 1 0 , x = - 1
Investigue a continuidade nos pontos indicados: f x = x 2 - 3 x + 7 x 2 + 1 , e mx = 2
Construa o gráfico e analise a continuidade das seguintes funções: f x = ln x + 1 , x ≥ 0 - x, x0