Construa o gráfico e analise a continuidade das seguintes funções:
Passo 1
Vamos construir o gráfico, temos que quando a função tem valor igual a , então vamos substituir valores de na função para encontrar os pontos:
E assim por diante.
Já para valores de a função tem valor de , então vamos ter:
E assim por diante.
Colocando esses pontos no gráfico vamos ter:
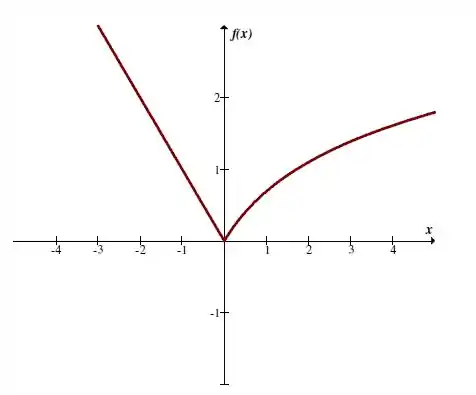
Assim vamos ter uma função contínua em todo o seu domínio, em todo o conjunto dos números reais.
Resposta
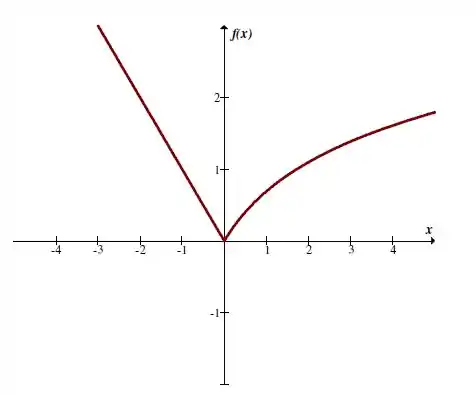
A função contínua em todo o seu domínio, em todo o conjunto dos números reais.