Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 18

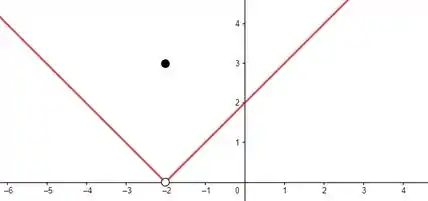
Nos exercícios de a , faça um esboço do gráfico da função; então, observando onde há quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre por que a Definição não é satisfeita em cada descontinuidade

Passo 1

Bora lá. Pra gente descobrir se uma função é ou não contínua a gente tem que fazer:

E isso vale pra qualquer , tranquilo? Vamos nos preocupar só com o porque é o valor de que a lei de formação da função muda:

Como esse resultado não faz sentido, a função não vai estar definida pra !

Passo 2

Pra esboçar essa função, note que a lei de formação é do módulo de uma reta. Pela definição de módulo:

O que é o mesmo que:

Marcamos ainda ponto já que ele está definido e tiramos o ponto já que ele nã oestá

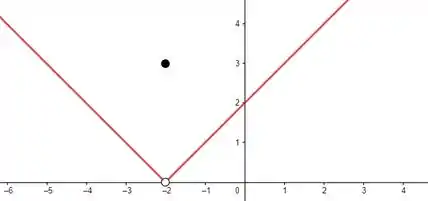
Resposta

Função não é contínua em

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1-4. Seja f a função cujo gráfico é dado. Em quais (se houver) dos intervalos seguintes f é contínua?3. a) [ 1 ,3 ] b) ( 1 ,3 ) c) [ 1 ,2 ] d) ( 1 ,2 ) e) [ 2 ,3 ] f) ( 2 ,3 )

1-4. Seja f a função cujo gráfico é dado. Em quais (se houver) dos intervalos seguintes f é contínua?1. a) [ 1 ,3 ] b) ( 1 ,3 ) c) [ 1 ,2 ] d) ( 1 ,2 ) e) [ 2 ,3 ] f) ( 2 ,3 )

1-4. Seja f a função cujo gráfico é dado. Em quais (se houver) dos intervalos seguintes f é contínua?2. a) [ 1 ,3 ] b) ( 1 ,3 ) c) [ 1 ,2 ] d) ( 1 ,2 ) e) [ 2 ,3 ] f) ( 2 ,3 )

39- Prove que f x = x 3 5 é contínua em toda parte, justificando cuidadosamente cada passo.

45-Dê um exemplo de uma função que está definida em todo ponto de um intervalo fechado e cujos valores nas extremidades têm sinais opostos, mas para a qual a equação f x = 0 não tem solução no interva