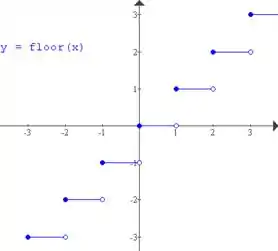
Nos exercícios de a , faça um esboço do gráfico da função; então, observando onde há quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre por que a Definição não é satisfeita em cada descontinuidade

Primeira coisa que a gente tem que fazer é definir essa função. Ela tem essa carinha:

Em outras palavras, você pega qualquer valor de , joga na função, e ela retorna o maior valor inteiro menor que o escolhido. Por exemplo:

Nota o seguinte agora:

Sendo assim, essa função vai ter uma cara de escadinha:

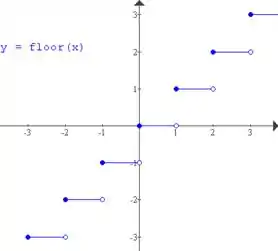
Como pra uma função ser contínua tem que ser válido...

...e nesse caso não é, a função vai ser descontínua. Isso vale pra todos os valores de mas como podemos ver pelo gráfico, existem infinitos pra testar. Veja por exemplo pra:

Como esse resultado não faz sentido, provamos ser descontínua.