Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 13
Nos exercícios de a , faça um esboço do gráfico da função; então, observando onde há quebras no gráfico, determine os valores da variável independente nos quais a função é descontínua e mostre por que a Definição não é satisfeita em cada descontinuidade
Passo 1
Opa uma função definida por partes! Bem, pra uma função ser contínua tem que ser válido:
E isso pra qualquer que a gente escolha. Mas aí, testamos todos os possíveis? Nem, pode relaxar. Como a função só muda de lei de formação em , fazemos:
E opa, tem algo errado aí! Não da pra ser uma verdade. Sendo assim a função é descontínua em
Passo 2
Pra conseguirmos esboçar só precisamos notar na lei de formação porque as outras duas não dependem de . Veja que essa lei de formação não pode assumir valores negativos e que:
Sendo assim já da pra ter uma ideia de pra onde tende. Traçando essa curva e marcando os pontos, temos:
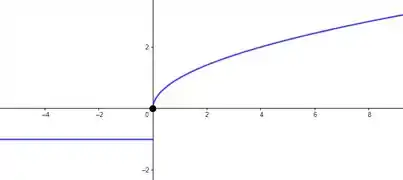
Resposta
Função não é contínua em .
