Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 2.3 - Ex. 26

Nos exercícios 24 a 28, encontre uma curva geratriz e o eixo da superfície de revolução dada. Faca um esboço da superfície

26.

z 4 - 16 x 2 = 16 y 2

Passo 1

Oiii a todos que estão ingressando no mundo do cálculo de várias variáveis. Quando aprendemos a fazer gráficos em cálculo 1, aprendemos vários truques. Inclusive, se você já está mais sagaz, de olhar para uma função e concluir “ah isso aqui, tem um jeito de círculo”, por exemplo, rs. Se você ainda não pegou essa sagacidade, relaxe! Isso vem apenas com o tempo e após vários exercícios.

Uma dica que dou é usar muito uma calculadora gráfica. Isso ajuda absurdamente na compreensão da geometria do seu sistema.

Passo 2

Primeiramente, esse livro tem um pequeno erro de edição, afinal essa função

z 4 - 16 x 2 = 16 y 2

Não é possível renderizar graficamente. Mais apropriado seria

z 2 - 16 x 2 = 16 y 2

Essa função sim temos como trabalhar. Plotando esse gráfico obtemos

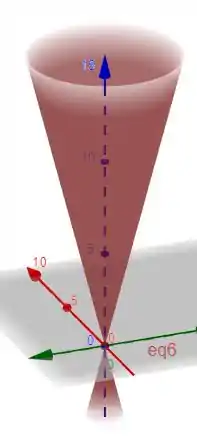
Que é um hiperboloide de 2 folhas.

Lembra de quando fizemos o seguinte quando estávamos em 2D que riamos ir para 3D

V a r i a v e l   e i x o = V a r i a v e l   I n d e p e n d e n t e   2 + V a r i a v e l   I n d e p e n d e n t e   2

Isso vai ser útil para guiar a gente agora. Percebe só. Pelo gráfico, podemos ver que o eixo de simetria é o z, então poderíamos fazer

z 2 - 16 x 2 = 16 y 2

z 2 = 16   x 2 + y 2

E dizer que nossa curva original era

z 2 = 16   x 2

E rotacionamos em z. ou

z 2 = 16   y 2

E rotacionamos em z. Da no mesmo e ambas nos dão o mesmo resultado.

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

z 2 = 16   x 2

E rotacionamos em z. ou

z 2 = 16   y 2

E rotacionamos em z.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A partir da Figura 19 parece que a limaçon perde sua covinha quando c = 1 2 . Demonstre isto.
A figura mostra o gráfico de r como uma função de θ em coordenadas cartesianas. Use-o para esboçar a curva polar correspondente.
No Exemplo 11 os gráficos sugerem que a limaçon r = 1 + c sen ⁡ θ tem um laço interno quando c1 . Demonstre que isso é verdadeiro e encontre os valores de θ que correspondam ao laço interno.
Mostre que a curva r = 2 - cossec ⁡ θ (também uma conchoide) tem a reta y = - 1 como uma assíntota horizontal mostrando que lim r → ± ∞ ⁡ y = - 1 . Use esse fato para ajudar a esboçar a conchoide.
Mostre que a curva r = sen ⁡ θ tg ⁡ θ (denominada cissoide de Diocles) tem a reta x = 1 como uma assíntota vertical. Mostre também que a curva está inteiramente dentro da faixa vertical0 ≤ x ≤ 1 . Use