No Exemplo 11 os gráficos sugerem que a limaçon tem um laço interno quando . Demonstre que isso é verdadeiro e encontre os valores de que correspondam ao laço interno.
Passo 1
Olá, meu amigo. Vamos resolver mais uma atividade.
Aqui nos é dito que a limaçon, com equação:
E gráfico abaixo, possui um laço interno quando:
Devemos então provar que isso é verdade.
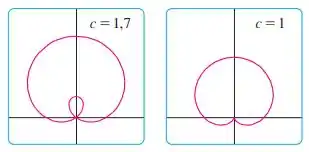
Para demonstrarmos isso precisamos entender o que causa esse laço interno.
O laço interno é causado por valores negativos de que fazem com que a curva se desloque ao sentido oposto ao da angulação de .
Sabendo que o laço é causado por valores negativos de precisamos provar que nossa função só assume valores negativos para .
Passo 2
Seja:
Vamos lá, dando uma olhada na equação temos uma constante somando uma função de que é , quando que teremos valores negativos de ?
Ou seja, quando que ? Quando , manipulando essa inequação vamos descobrir que
Sabemos que o tem valor limitado entre e . Pra deixar mais bonito podemos escrever assim:
Se multiplicarmos por chegamos à conclusão de que se for positivo,
ou seja varia de até .
Já que queremos que seja menor que , faz sentido analisarmos o menor valor de , para que o laço apareça. Então, seguindo essa lógica o menor valor , tem que ser menor que
Multiplicando por , lembrando que em uma inequação, se fizermos isso temos que inverter a comparação
Mas isso só vale porque analisamos para valores positivos de , se for negativo então varia de até e o menor valor possível seria o próprio . Então se for negativo
Podemos aqui também multiplicar por para acharmos uma forma mais geral
Então concluímos que:
- Se :
- Se
Já que dependendo do sinal de , temos sinais diferentes também na inequação, o que realmente importa é o valor absoluto de , ou seja, seu módulo:
Passo 3
Para descobrir os valores de que são responsáveis pelo laço vamos usar os limites dos valores negativos de , esses valores começam após
Dividindo por
Aplicando a função inversa do seno
O outro limite, quando volta a ser positivo acontece no seu ângulo suplementar. Sabemos que se e são suplementares, então nosso outro valor de é
O laço acontece entre os ângulos e .
Resposta
Ver o desenvolvimento.