Mostre que a curva (denominada cissoide de Diocles) tem a reta como uma assíntota vertical. Mostre também que a curva está inteiramente dentro da faixa vertical. Use esses fatos para ajudar a esboçar a cissoide.

Primeiramente achando vamos manipular a equação

Para isso usaremos

Substituindo o nessa equação temos que

Sabemos que , então

Agora a gente precisa de uma sacada monstra, precisamos calcular o quando , mas nós temos o em função de Para conseguirmos calcular vamos ter que achar qual valor de para que nosso .

Pensando primeiro no . Para que isso ocorra, precisamos que . Primeiro precisamos que seja positivo e pra que isso ocorra vamos pensar o seguinte:

Para isso ser positivo, ou tanto o seno e o cosseno são positivos, ou só seno é negativo.

Outra coisa que precisamos é que o denominador tenda a , para que nossa função tenda ao infinito. Então e isso ocorre em . Mas para que o cosseno seja positivo .

Então vamos lá:

E para calcular esse limite, basta substituir

Para , basta pegarmos o outro lado de que já muda o sinal da função já que quando o cosseno é negativo. Então

Então tá provado que é uma assíntota da função .

Para mostrar que a função está contida entre as faixas e , dividimos a análise em cada quadrante do plano polar.

1. Primeiro Quadrante (​):

A função é positiva porque tanto o seno quanto o cosseno são positivos nesse intervalo.

Começa em (origem) e segue o limite da assíntota . Portanto, a função é menor que nesse quadrante.

2. Segundo Quadrante ():

A função é negativa porque o cosseno é negativo nesse intervalo.

Nesse quadrante, os valores negativos indicam que a curva se move em direção ao quarto quadrante (onde ).

Começa no limite da assíntota e aumenta até alcançar .

3. Terceiro Quadrante (​):

A situação é similar ao segundo quadrante devido às propriedades do cosseno.

A função permanece negativa e começa no limite da assíntota , crescendo em direção a .

4. Quarto Quadrante ():

Como no primeiro quadrante, a função é positiva devido ao cosseno e seno positivos.

Começa em e segue o limite da assíntota , mantendo-se menor que .

Essa abordagem quadrante por quadrante permite demonstrar que a função permanece entre as faixas e ao longo de todo o intervalo .

A cissoide de Diocles tem a reta como assíntota vertical, pois cresce indefinidamente quando se aproxima de ​. A curva está inteiramente contida na faixa vertical , como demonstrado pela equação em coordenadas cartesianas. Para variando de a ​, os valores de variam de a , confirmando que a curva não ultrapassa essa faixa.

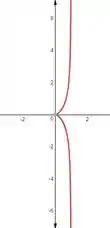
O esboço do gráfico mostra uma curva suave que se estende de a , aproximando-se verticalmente da reta sem cruzá-la. Este comportamento ilustra claramente a relação da cissoide com sua assíntota e sua localização na faixa vertical especificada.