Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 50
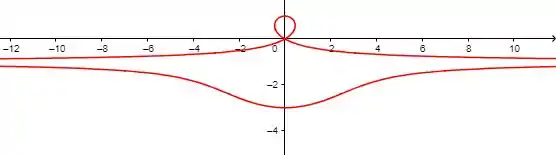
Mostre que a curva (também uma conchoide) tem a reta como uma assíntota horizontal mostrando que . Use esse fato para ajudar a esboçar a conchoide.
Passo 1
Antes de tudo, o que é essa tal de assíntota?
Assíntota é geralmente uma reta, que em um limite a função que eu tô analisando se aproxima deste valor. Um bom exemplo é a função
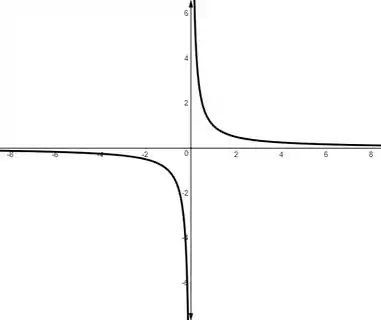
Podemos falar que a reta é uma assíntota vertical pra essa função, pois no essa função tente a se comportar como essa reta.
As coordenadas polares e coordenadas cartesianas se relacionam da seguinte forma:
Assim como na questão anterior temos que provar uma assíntota. Desta vez vamos provar que , para isso precisamos provar o seguinte limite:
Passo 2
Para calcular esse limite precisamos achar em função de , . Para isso vamos manipular a equação
Sabemos que , substituindo temos
Agora precisamos usar , isolando o temos que , substituindo na equação
Multiplicando a equação por
Subtraindo de toda a equação temos
Colocando agora em evidência
Por fim, dividindo a equação por nós chegamos no nosso objetivo
Passo 3
Vamos agora calcular o limite
Colocando o em evidência do lado de baixo e simplificando com o do numerador
E então temos nossa resposta para o limite
Passo 4
Agora que sabemos que é uma assíntota para , precisamos saber como a função se comporta para ir ao plano.
Já em temos uma indeterminação, já que . No limite
Então a função aumenta até zerar em onde a e então a função continua a aumentar até onde a função vale . Então ela começa a diminuir novamente ate zerar em e continua a diminuir até onde temos outra indeterminação:
No limite a função assume outro valor
E então vai diminuindo até chegar em quando e começa a aumentar novamente chegando em outra indeterminação quando
E então reiniciando o ciclo.
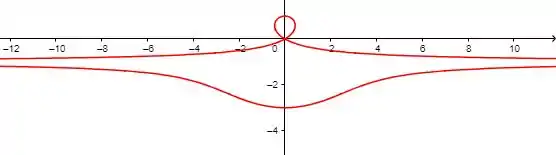
Passo 5
No plano ficamos com algo assim:
Resposta
Ver o desenvolvimento
