Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.1 - Ex. 29
Nos exercícios de 27 a 32, ache o vértice, o foco, uma equação do eixo e uma equação da diretriz da parábola dada. Faça um esboço do gráfico.
Passo 1
Vamos reescrever a equação dada de modo que fique:
Passo 2
Completando quadrado dos termos envolvendo no primeiro membro:
Assim, conseguimos extrair todas as informações que queremos.
Passo 3
Como temos uma equação do tipo:
Onde h e k representam as coordenadas x e y da parábola, respectivamente, logo nosso vértice é:
Equação do eixo:
Como a equação que obtemos é do tipo:
Temos que o eixo da parábola é paralelo ao eixo x passando pelo vértice, logo a equação do eixo é dada por:
O foco está em:
Como o vértice está no ponto médio entre a reta diretriz e o foco e a distância entre o vértice e o foco é igual a p, assim a distância entre o vértice e a reta diretriz é igual p.
A reta diretriz nesse caso, levando em conta o tipo de equação que temos, é paralela ao eixo y. Assim temos que a equação da reta diretriz é:
Passo 4
O gráfico que representa a equação da parábola é da seguinte maneira:
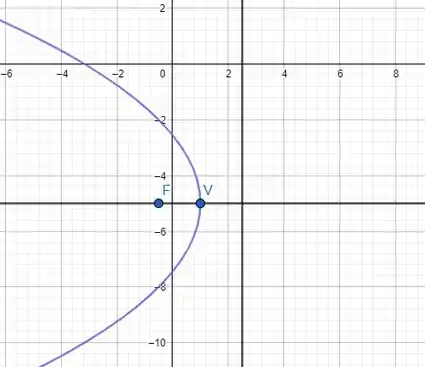
Resposta
Vértice:
Foco:
Equação do eixo:
Equação da diretriz: