Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 27
Nos exercícios a esboçar o gráfico das curvas dadas em coordenadas polares.
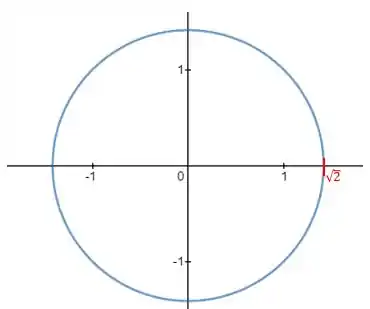
Passo 1
Observando-se o formato da equação dada, é possível lembrar que esta representa o gráfico de uma circunferência centrada no pólo, já que possui uma equação da forma:
Onde o valor de representa o raio dessa circunferência.
Passo 2
Normalmente, seria feita a análise do valor de para cada valor de . Neste caso, isso não é necessário já que a variável independe de e, portanto, pode-se fazer o esboço do gráfico diretamente com as informações já adquiridas.
Passo 3
Dessa forma, a circunferência centrada no pólo e com raio será dada por:
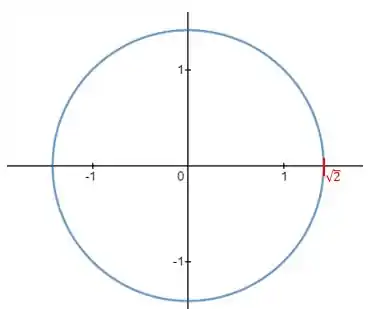
Resposta
Exercícios de Livros Relacionados
Determine as áreas das superfícies geradas girando as curvas nos Exercícios 21 e 22 em torno dos eixos indicados. x = t 2 2ey = 2 t ; 0 ≤ t ≤ 5 ; e i x ox
Determine as áreas das superfícies geradas girando as curvas nos Exercícios 21 e 22 em torno dos eixos indicados. x = t 2 + 1 2 tey = 4 t ; 1 2 ≤ t ≤ 1 ; e i x oy
Encontre equações polares para os círculos nos Exercícios 33-36. Esboce cada círculo no plano coordenado e rotule-o com suas equações cartesianas e polares. x 2 + y 2 + 4 x = 0
Esboce as retas nos Exercícios 23-28. Determine também uma equação cartesiana para cada reta. r = - 3 2 cos sec θ
Encontre equações polares para os círculos nos Exercícios 33-36. Esboce cada círculo no plano coordenado e rotule-o com suas equações cartesianas e polares. x 2 + y 2 - 3 x = 0