Identidade para : A figura (1) estabelece a identidade para . Para estabelecer a identidade para o restante de [-1,1], verifique, por cálculo direto, que ela é verdadeira para e -1. Em seguida, para valores de em (-1,0) faça e aplique as equações (2) e (3) à soma .

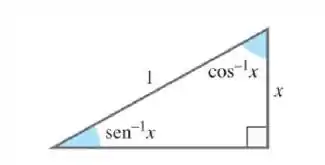
Figura (1)

Equação (2)

Equação (3)

Aqui vamos só jogar os valores e -1 na equação e ver que eles funcionam.

Para :

.

O arco cujo seno vale 0 é o próprio 0 e o arco cujo cosseno vale 0 é (existem outros, mas eu só preciso de um deles pra provar).

Então, , o que prova que é verdade.

Para :

O arco cujo seno vale 1 é o e o arco cujo cosseno vale 1 é o 0.

Então, , o que prova que é verdade.

Para :

O arco cujo seno vale -1 é o e o arco cujo cosseno vale -1 é o .

Então, . Como esse só indica que você deu duas voltas a mais no Círculo Trigonométrico e caiu no mesmo arco, temos que , o que prova que é verdade.

Aqui, vamos dizer que e em (-1,0). Por que esse ? Porque o tá em um intervalo negativo e a gente representa um número negativo como menos um número positivo, por isso que . Só que a gente só sabe que as equações dadas valem pra valores positivos de , e não pra negativos e o que a gente quer provar é que vale pra negativos também. Então saca só:

Queremos mostrar que: , onde é um valor negativo. Então, vamos começar olhando pra soma:

, porque, pela equação (2), , onde .

Mas lembre que, pela equação (3), , porque é um número positivo.

Então:

Até aí você entendeu? Vamos continuar:

(nessa última parte aqui eu só coloquei os pertinhos)

Ok, aqui chegamos em mais um detalhe: a função seno é ímpar, ou seja, . Então, o que nos dá que . Logo:

. Assim, concluímos que e, como é um número negativo, provamos que a igualdade vale pra negativos também.