Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.6 - Ex. 75d
Inicie o gráfico com . Determine uma equação para o gráfico que resulte em uma translação de 4 unidades para baixo e 2 unidades para a direita.
Passo 1
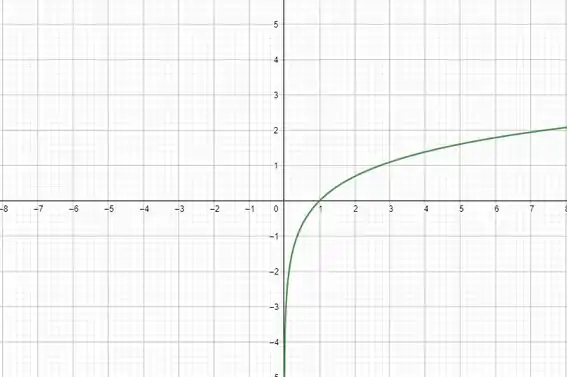
E aí galera, tudo bom? Essa questão é bem simples, vai ser bem rapidinho eu prometo. O que ele tá querendo é que você pegue o gráfico do e faça modificações pra que esse gráfico apareça 4 unidades pra baixo e 2 unidades para a direita, ou seja, a gente tem que “empurrar” ele 4 unidades pra baixo e 2 unidades pra direita, entendeu? Então bora pro PASSO 2! Mas antes saca só: esse é o gráfico “original” que a gente vai empurrar.
Passo 2
Gente é muito simples, tem uma regrinha que é o seguinte:
- Se você quer empurrar um gráfico pra direita, dentro da equação, ou seja, dentro do , você vai subtrair as unidades que você quer empurrar.
- Se você quer empurrar um gráfico pra baixo, do lado de fora da equação, ou seja, fora do , você vai subtrair as unidades que você quer empurrar.
Como assim? Desse jeito, se eu quero deslocar pra baixo 4 unidades e pra direita 2 unidades no gráfico, dentro do eu tenho que tirar 2 unidades e fora do eu tenho que tirar 4 unidades, ou seja, .
Agora se eu quiser empurrar pra esquerda, aí ao invés de menos (-), eu coloco mais (+), beleza?
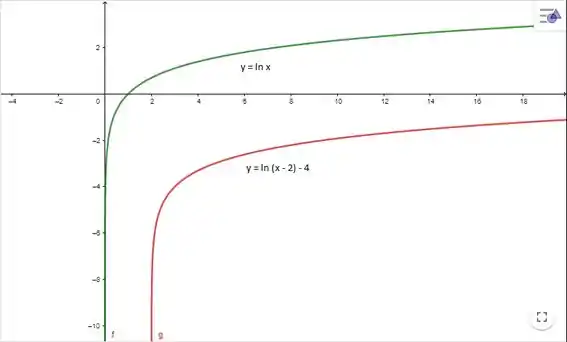
Viu que ele foi “empurrado” 2 unidades pra direita e 4 unidades pra baixo?
E é só isso gente, não tem mistério nenhum.
Resposta
.