Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 42

Nos exercícios 35 a 43, determinar os valores máximo e mínimo da função dada, na região indicada.

42. ; e .

Passo 1

Então pessoal, antes de começarmos a análise, vamos fazer um esboço da região do domínio que queremos analisar, ok?

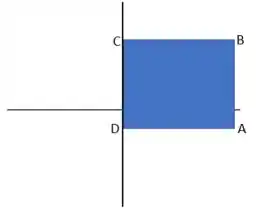
De início temos que analisar os pontos críticos que existem no interior da região, galera. Para fazermos isso devemos derivar parcialmente nossa função e igualar os resultados a zero, desse jeito aqui ó:

Igualando a zero, teremos:

Da segunda equação podemos tirar que , certo? Substituindo na primeira, teremos:

Para temos que e para temos que . Sendo assim, os pontos críticos são: e . Vamos guardar essa informação!

Passo 2

Agora que analisamos o interior, vamos partir para as fronteiras! Para o segmento temos que , . Dessa forma:

Derivando e igualando a zero:

Desse resultado tiramos o ponto . Para o segmento temos que , . Dessa forma:

Derivando e igualando a zero:

Desse resultado tiramos o ponto .

Tudo bem, metade dos segmentos foram encontrados, agora vamos para os dois últimos!

Passo 3

Para o segmento temos que , . Dessa forma:

Derivando e igualando a zero:

Desse resultado tiramos o ponto . Por fim, para o segmento temos que , . Dessa forma:

Derivando e igualando a zero:

Não conseguimos tirar valores reais desse resultado! Em resumo, pelos resultados que obtivemos, se substituirmos os valores na função que nos foi dada teremos que:

Os pontos e são pontos de mínimo e valem e os pontos e são pontos de máximo e valem .