Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 11.2 - Ex. 41
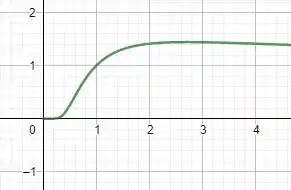
Nos exercícios 41 e 42, faça um esboço do gráfico de , determinando primeiro os extremos relativos de e as assíntotas horizontais do gráfico, se existirem.
41.
Passo 1
Se esboçarmos o gráfico de , teremos algo desse tipo:
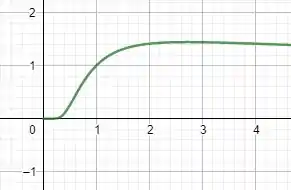
Para descobrirmos os extremos relativos de , termos que utilizar o raciocínio de máximos e mínimos! O racícionio consiste em derivarmos e igualarmos a zero para analisar seus pontos críticos. Tá confuso? Prometo que não é tão difícil assim, bora lá! Antes de derivarmos, vamos escrever de uma forma que nos possibilite derivar, se liga:
Aplicando em ambos os lados da função, teremos:
Passo 2
Agora que temos uma função mais tranquila de ser derivada, derivando-a teremos:
Se igualarmos essa função a zero, notaremos que quando . Sendo assim, se substituirmos esse ponto crítico na função original, teremos:
Que é exatamente o extremo relativo que procurávamos.
Passo 3
Para determinarmos as assíntotas horizontais da função, basta aplicarmos o limite da função tendendo ao infinito, se liga:
Aplicando a regra de L’Hôspital, teremos:
Como utilizarmos a função com logaritmo, então:
Sendo assim, é uma assíntota horizontal.
Resposta
