Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 20
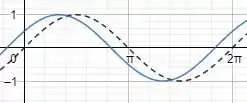
Faça os gráficos das funções nos Exercícios 13-22. Qual o período de cada função?
Passo 1
Então galera, quando temos uma função que apresenta uma soma ou subtração diretamente na variável, ou seja, uma função desse tipo aqui:
Isso implica que o gráfico da função vai ser deslocado ou transladado horizontalmente, tudo bem? Se for uma soma o gráfico vai ser deslocado para a esquerda. Se for uma subtração o gráfico vai ser deslocado para a direita. Como no nosso caso há uma soma, então haverá um deslocamento de para a esquerda. Se liga em como vai ficar o gráfico disso:
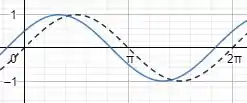
No qual a função pontilhada é e a função azul é .
Passo 2
Por fim devemos descobrir o período da função que nos foi dada. Para calcularmos o período é beeem tranquilão! O período é dado pela razão:
No qual é o número que acompanha a variável na função. No nosso caso , logo:
Resposta
