Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.3 - Ex. 59
Nos Exercícios 55-62, faça o gráfico da função e determine o seu valor médio ao longo do intervalo dado.
59. em
Passo 1
Então galera, para determinarmos o valor médio de uma função, assim como discutido na seção 3 do George, basta calcularmos isso aqui ó:
E para calcularmos o valor dessa integral, assim como discutido nessa mesma seção, basta lembrarmos das seguintes integrais:
Passo 2
Se plotarmos o gráfico dessa função no intervalo apresentado pela questão, teremos o seguinte:
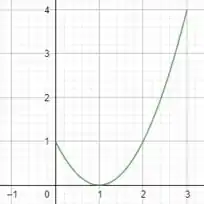
Passo 3
Por fim, calculando o valor médio:
Resposta
Exercícios de Livros Relacionados
Use as propriedades das integrais, junto com os exercícios 27 e 28 , para demonstrar a desigualdade. ∫ 0 π 2 x sen x d x ≤ π 2 8
Suponha que f tenha uma valor mínimo absoluto m e um valor máximo absoluto M . Entre quais dois valores ∫ 0 2 f x d x deve ficar? Que propriedade das integrais lhe permitem tirar esta conclusão?
Use as propriedades das integrais para verificar a desigualdade sem calcular as integrais. 2 ≤ ∫ - 1 1 1 + x 2 d x ≤ 2 2
Use a Propriedade 8 para estimar o valor da integral. ∫ 0 2 x 3 - 3 x + 3 d x
Se f for contínuaem a , b , mostre que∫ a b f x d x ≤ ∫ a b f x d x [Sugestão: - f x ≤ f x ≤f x .]