Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.2 - Ex. 9
Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo das regiões limitadas pelas curvas e retas a seguir.
para
Passo 1
Lembrando do método da casca que é um método para calcular o volume de uma região segundo a fórmula:
Como o volume é em torno de , o raio da casca é igual a . Já a altura da casca é igual a diferença entre as curvas e .
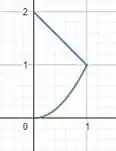
Assim,
Passo 2
Calculando a integral:
Resposta
Exercícios de Livros Relacionados
Se a região mostrada na figura a seguir é girada em torno do eixo y formando um sólido, use a Regra de Simpson, com n = 8 , para estimar o volume do sólido.
Use o método das cascas cilíndricas para encontrar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. y = e x , y = e - x , x = 1 ; e mt o r n od oe i
Use o método das cascas cilíndricas para encontrar o volume gerado pela rotação da região delimitada pelas curvas dadas ao redor dos eixos especificados. x = ln y ,y = 1 ,y = π ; e mt o r n od oe i
Use o método das cascas cilíndricas para encontrar o volume gerado pela rotação da região delimitada pelas curvas dadas ao redor dos eixos especificados. y = e - x ,x = 0 ,y = π ; e mt o r n od oe i x
Use o método das cascas cilíndricas para encontrar o volume gerado pela rotação da região delimitada pelas curvas dadas ao redor dos eixos especificados. y = cos π x 2 ,y = 0 ,0 ≤ x ≤ 1 ; e mt o r n