Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.2 - Ex. 10
Nos Exercícios 7-14, escreva os primeiros termos de cada série para mostrar como a série começa. Então, calcule a soma da série.
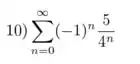
Passo 1
Fala galerinha, temos o somatório:
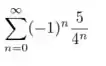
Nesse caso a primeira parte do exercício consiste em substituição simples dos termos, basta você obedecer o valor de onde a somatória começa, e depois somaremos a série.
Os primeiros termos são:
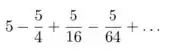
Passo 2
A soma da série pode ser feita utilizando a seguinte expressão:
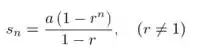
Substituindo para o nosso caso:
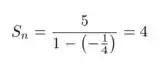
Prontinho!
Resposta
Exercícios de Livros Relacionados
Determine se a série é convergente ou divergente expressando s n como uma soma telescópica (como no Exemplo 6). Se for convergente, calcule sua soma. ∑ n = 1 ∞ 2 n 2 + 4 n + 3
Determine se a série é convergente ou divergente expressando s n como uma soma telescópica (como no Exemplo 6). Se for convergente, calcule sua soma. ∑ n = 2 ∞ 2 n 2 - 1
Encontre os valores de x para os quais a série converge. Calcule a soma da série para esses valores de x . ∑ n = 1 ∞ x n 3 n
Determine se a série é convergente ou divergente. Se ela for convergente, calcule sua soma. ∑ n = 1 ∞ [ 2 0,1 n + 0,2 n ]
Se a n -ésima soma parcial de uma série ∑ n = 1 ∞ a n for s n = n - 1 n + 1 Encontre a n e ∑ n = 1 ∞ a n .