Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.Revisão - Ex. 81
Nos exercícios 81 e 82, ache os valores das constantes a e b que tornam contínua a função f em e faça um esboço do gráfico de f.
81)
Passo 1
O exercício solicita que se calcule as constantes a e b de forma que a função se torne contínua em reais.
Para descobrir as constantes a e b iremos montar um sistema de equações utilizando os limites laterais.
Resolvendo o sistema das equações (I) e (II), teremos:
Passo 2
O esboço do gráfico da função será,
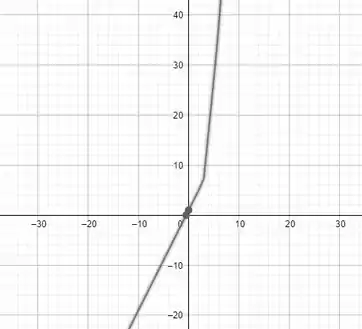
Resposta
Os valores das constantes são .
O gráfico da função é:
Exercícios de Livros Relacionados
Quais das seguintes funções f tem uma descontinuidade removível em a ? Se a descontinuidade for removível, encontre uma função g que seja igual a f para x ≠ a e seja contínua ema . a f x = x 4 - 1 x -
91)(a) Prove que se lim h → 0 f x + h = f x , então lim h → 0 f x + h = lim h → 0 f x - h (b) Mostre que o inverso do teorema (2) não é verdadeiro, dando exemplo de uma função para a qual lim h
93) Se o domínio de f for o conjunto de todos os números reais e se f for contínua em 0, prove que se f a + b = f a + f b para todo a e b, então f será contínua em todo número.
Os exercícios de 95 a 98 referem-se à Secção Suplementar 2.9. Nós exercícios 95 e 96, use os Teoremas de 2.7.1 a 2.9.1, mas não o Teorema 9 (o limite de um quociente), para encontrar o limite.95) lim