Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.1 - Ex. 38
Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas.
Passo 1
Bom galera, antes de começar, vamos desenhar esta situação !
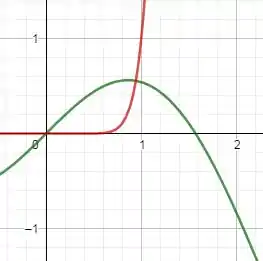
Agora vamos chamar:
Já sabemos como se calcula área sobre as curvas, não é?
E quanto aos intervalos de integração?
Nós vamos calcular a área entre os pontos onde eles se cruzam. E onde se cruzam?
Vamos igualar as funções e descobrir, ok?
Então:
Passo 2
Como nossa variável é o x nosso intervalo de integração vai de
Agora ficou fácil, não é?
Substituindo as funções:
Vamos separar a integral:
A outra integral nós teremos que resolver por substituição:
Então:
Aplicando o intervalo:
Então:
Resposta
Exercícios de Livros Relacionados
Desenhe a curva dada (coordenadas polares ). ρ = e - θ , θ ≥ 0
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas