Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 46

Esboce a região no plano xy definida pelas inequações x - 2 y 2 ≥ 0 ,   1 - x - y ≥ 0 e encontre sua área.

Passo 1

Bom galera, antes de começar, vamos isolar o x!

x ≥ 2 y 2

Para plotar o gráfico vamos usar:

x = 2 y 2

A próxima inequação é:

- x ≥ - 1 + | y |

Vamos multiplicar esta última por -1:

x ≤ 1 - | y |

Para plotar o gráfico:

x = 1 - | y |

Como nós temos o módulo devemos analisar para o y positivo e negativo:

x = { 1 - y ,                 s e   y ≥ 0 1 + y ,             s e   y < 0

Desenhando:

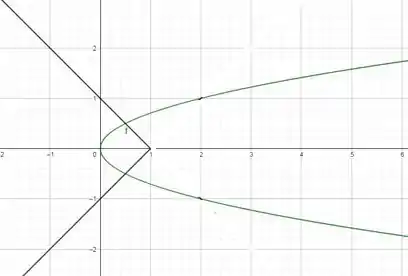
Passo 2

Agora vamos chamar:

f ( y ) = 2 y ²                           ( v e r d e ! )

g y = 1 - | y |               ( p r e t o ! )

Já sabemos como se calcula área sobre as curvas, não é?

E quanto aos intervalos de integração?

Nós vamos calcular a área entre os pontos onde eles se cruzam. E onde se cruzam?

Vamos igualar as funções e descobrir, ok?

Começando por y ≥ 0 :

1 - y = 2 y ²

2 y ² + y - 1 = 0

Fazendo Bhaskara:

y ' = 1 2           e           y ' ' = - 1

Como estamos falando de y positivo usaremos y ' = 1 2 .

Antes de fazer y negativo vamos observar que o lado positivo é simétrico ao lado negativo, então para calcular a área basta nós fazermos a integral de um dos lados e multiplicar por 2, tudo bem?

Sendo assim, o intervalo de integração será y de 0 → 1 2 :

A = ∫ 0 1 2 f y - g y . d y

Substituindo as funções:

A = 2 ∫ 0 1 2 ( 1 - y ) - 2 y ² . d y

= 2 ∫ 0 1 2 1 - y - 2 y ² . d y

Vamos separar a integral:

= 2 ∫ 0 1 2 1 . d y - ∫ 0 1 2 y . d y - ∫ 0 1 2 2 y 2 . d y

= 2 y - y 2 2 - 2 y 3 3 1 / 2 0

Aplicando o intervalo:

= 2 . 1 2 - 1 2 2 2 - 2 1 2 3 3 - 2 . 0 - 0 2 2 - 2 . 0 3 3

= 2 1 2 - 1 8 - 1 12

Tirando MMC:

= 2 1 2 - 3 - 2 2 4 = 7 12

Então:

A = 7 12

Resposta

A = 7 12

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região entre a curva y = sec 2 ⁡ x , - π 4 ≤ x ≤ π 4 , e o eixo x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região limitada pela parábola y = x - x 2 e pela reta y = - x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada.A região no primeiro e quarto quadrantes, delimitadas pelas curvas y = 1 1 + x 2 e
16- Determine o centro de massa de uma placa fina que abrange a região limitada abaixo pela parábola y = x 2 e acima pela reta y = x , se a densidade da placa no ponto ( x , y ) for δ x = 12 x .
Nos Exercícios 1-14, determine o centro de massa de uma placa fina de densidade constante δ que abranja a região dada. A região limitada pelas parábolas y = 2 x 2 - 4 x e y = 2 x - x 2 .